2.4: Conditional Probability

Conditional Probability

Imagine you’re playing a game with a fair six-sided die. Someone rolls the die behind a screen and asks you, “What’s the probability that it’s a five?” Initially, you’d say $\frac{1}{6}$, right? There are six possible outcomes, and they’re all equally likely.

Now imagine if they then tell you, “The number is odd”? This new information changes things. Now you know the roll must be 1, 3, or 5. Out of these three possibilities, only one is a five. So your new answer would be $\frac{1}{3}$.

This scenario introduces us to conditional probability. Conditional probability asks: “What is the likelihood of an event, given that we know something else has already happened?” In probability notation, we write this as $P\left(A|B\right)$, which means “the probability of event A, given that event B has occurred.”

In our die example:
Event A: Rolling a five
Event B: Rolling an odd number
$P\left(A|B\right)$: The probability of rolling a five, given that we know the roll was odd

This concept of updating probabilities based on new information is crucial in many real-world applications, from weather forecasting to medical diagnoses.

Just as we did not need the computational formula in this example, we do not need it when the information is presented in a two-way contingency table, as in the next example.

Notice from the Try It Now 1 that $P\left(R|T\right)$ is not equal to $P\left(T|R\right)$.

These kinds of conditional probabilities are what insurance companies use to determine your insurance rates. They look at the conditional probability of you having accident, given your age, your car, your car color, your driving history, etc., and price your policy based on that likelihood.

Multiplication Rule

If we rewrite the conditional probability formula we have another tool to answer questions about probability
involving “and“.

In the definition above please note this does not mean we are saying $P\left(A\right)$ and $P\left(B\right)$ are equal to each other (or the conditional probabilities listed)

This manipulation of the conditional probability formula gives us another way of finding the probability of $A$ and $B$ (this also means the intersection of $A$ with $B$). It is not always needed when computing the probability of an intersection (the Addition Rule also can be manipulated or if we know the events $A$ and $B$ are independent we can use the rule from the previous section).

Let us put our knowledge of conditional probability, complements, and the multiplication rule to a test in this next Try It Now.

Independent Events

With conditional probability we saw how some events can often influence each other. However, sometimes events occur without affecting the likelihood of other events. We call these independent events.

Consider an example related to insurance company assessing risks on a home insurance policy:

$A$: A house experiences storm damage this year
$B$: The same house had a burglary last year

These events are likely independent because a past burglary doesn’t influence the chances of future storm damage.

Although typically we expect the conditional probability $P\left(A|B\right)$ to be different from the probability $P\left(A\right)$, it does not have to be true. When $P\left(A|B\right)=P\left(A\right)$, the occurrence of $B$ has no effect on the likelihood of $A$. Whether or not the event $B$ has occurred is independent of the event $A$.

Using algebra it can be shown that the equality $P\left(A|B\right)=P\left(A\right)$ holds if and only if the equality $P\left(A\cap B\right)=P\left(A\right)\cdot P\left(B\right)$ holds, which in turn is true if and only if $P\left(B|A\right)=P\left(B\right)$.

The formula in the definition has two practical but exactly opposite uses:

1. In a situation in which we can compute all three probabilities $P\left(A\right)$, $P\left(B\right)$, and $P\left(A\cap B\right)$, it is used to check whether or not the events $A$ and $B$ are independent:
   • If $P\left(A\cap B\right)=P\left(A\right)\cdot P\left(B\right)$, then $A$ and $B$ are independent.
   • If $P\left(A\cap B\right)\ne P\left(A\right)\cdot P\left(B\right)$, then $A$ and $B$ are not independent.
2. In a situation in which each of $P\left(A\right)$ and $P\left(B\right)$ can be computed and it is known that $A$ and $B$ are independent, then we can compute $P\left(A\cap B\right)$ by multiplying together $P\left(A\right)$ and $P\left(B\right)$: $P\left(A\cap B\right)=P\left(A\right)\cdot P\left(B\right)$.

Example 9

A jar contains 10 marbles, 7 black and 3 white. Two marbles are drawn without replacement, which means that the first one is not put back before the second one is drawn.

1. What is the probability that both marbles are black?
2. What is the probability that exactly one marble is black?
3. What is the probability that at least one marble is black?

---

Solution

A tree diagram for the situation of drawing one marble after the other without replacement is shown in “Tree Diagram for Drawing Two Marbles”. The circle and rectangle will be explained later, and should be ignored for now.

The numbers on the two leftmost branches are the probabilities of getting either a black marble, 7 out of 10, or a white marble, 3 out of 10, on the first draw. The number on each remaining branch is the probability of the event corresponding to the node on the right end of the branch occurring, given that the event corresponding to the node on the left end of the branch has occurred. Thus for the top branch, connecting the two $B$s, it is $P\left(B_2|B_1\right)$, where $B_1$ denotes the event “the first marble drawn is black” and $B_2$ denotes the event “the second marble drawn is black.” Since after drawing a black marble out of the jar there are 9 marbles left, of which 6 are black, this probability is $\frac{6}{9}$.

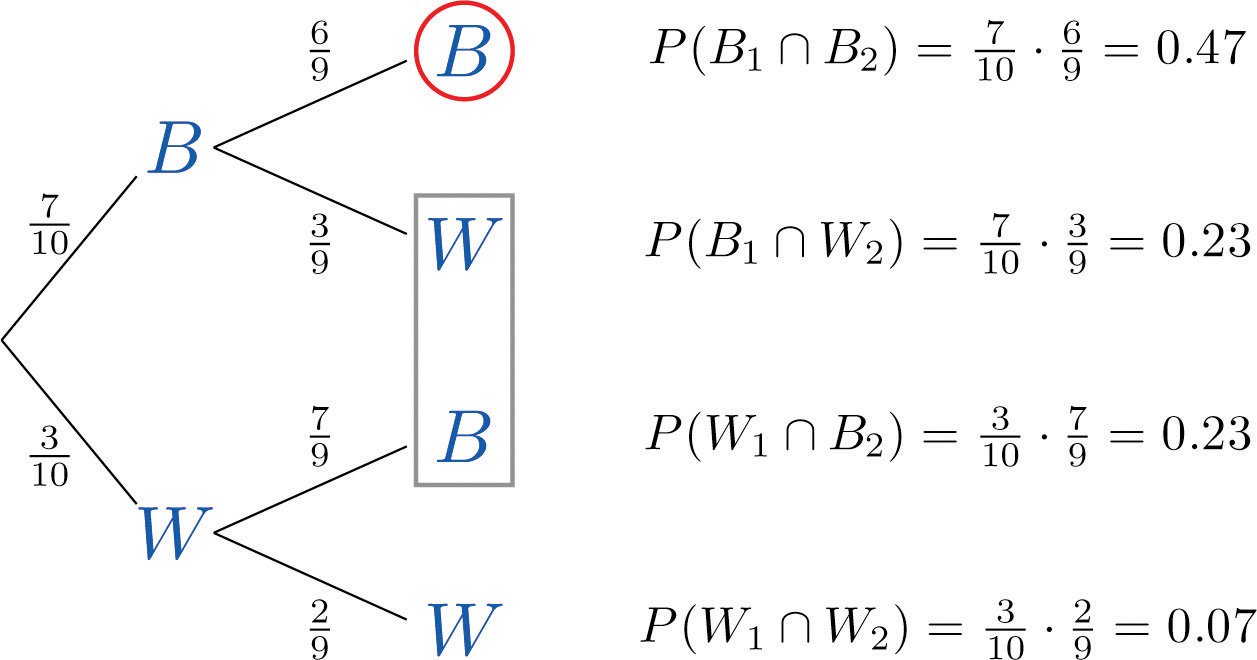
The number to the right of each final node is computed as shown, using the principle that if the formula in the Conditional Rule for Probability is multiplied by $P\left(B\right)$, then the result is

$$P\left(B\cap A\right)=P\left(B\right)\cdot P\left(A|B\right)$$

1. The event “both marbles are black” is $B1\cap B2$ and corresponds to the top right node in the tree, which has been circled. Thus as indicated there, it is:

   $$P\left(B_1\cap B_2\right)=P\left(B_1\right)\cdot P\left(B_2\right)=\frac{7}{10}\cdot \frac{6}{9}\approx 0.47$$

2. The event “exactly one marble is black” corresponds to the two nodes of the tree enclosed by the rectangle. The events that correspond to these two nodes are mutually exclusive: black followed by white $B_1\cap W_2$ is incompatible with white followed by black $W_1\cap B_2$. Thus in accordance with the Additive Rule for Probability we merely add the two probabilities next to these nodes. Thus the probability of drawing exactly one black marble in two tries is:

   $$P\left(B_1\cap W_2\right)+P\left(W_1\cap B_2\right)=0.23+0.23=0.46$$

3. The event “at least one marble is black” corresponds to the three nodes of the tree enclosed by either the circle or the rectangle. The events that correspond to these nodes are mutually exclusive, so as in part (b) we merely add the probabilities next to these nodes. Thus the probability of drawing at least one black marble in two tries is 0.47+0.23+0.23=0.93.

   $$P\left(B_1\cap W_2\right)+P\left(W_1\cap B_2\right)+P\left(B_1\cap B_2\right)=0.23+0.23+0.47=0.93$$

   Of course, this answer could have been found more easily using the Probability Law for Complements, simply subtracting the probability of the complementary event, “two white marbles are drawn,” from 1 to obtain 1−0.07=0.93.

WARNING!!!! Independent ≠ Disjoint (mutually exclusive)

The concepts of independent and mutually exclusive events are often confused.

For example let us take a standard 52-card deck. We will define two events

Event $B$: Drawing a black card
Event $H$: Drawing a heart

These events are mutually exclusive, since a card can’t be both black and a heart (red) at the same time.

$P\left(H\right)\text{=}\frac{13}{52}\text{=}\frac{1}{4}$, but if we know the card is black, $\text{P}\left(H|B\right)=0$.

This shows that knowing the card is black changes the probability of it being a heart. Therefore, these events are not independent.

Remember:

• For independent events: $\text{P}\left(A|B\right)=P\left(A\right)$
• For mutually exclusive events: $\text{P}\left(A\cap B\right)=0$

Exercises

1. For two events A and B, P(A)=0.73, P(B)=0.48, and P(A∩B)=0.29.
   1. Find P(A|B).
   2. Find P(B|A).
   3. Determine whether or not A and B are independent.
   Answer (click to Show/Hide)

   This problem uses the formula for conditional probability and the definition of independent events.

   The formula for conditional probability of event A given event B is:
   $$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

   a. Find $P(A|B)$

   We substitute the given values into the formula.
   $$P(A|B)=\frac{0.29}{0.48}\approx 0.604$$

   Answer (a): $P(A|B)\approx 0.604$.

   b. Find $P(B|A)$

   We use the corresponding formula for $P(B|A)$.
   $$P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{0.29}{0.73}\approx 0.397$$

   Answer (b): $P(B|A)\approx 0.397$.

   c. Determine whether or not A and B are independent.

   Two events A and B are independent if $P(A|B)=P(A)$. We can use our result from part (a) to check if this condition is met.

   Step 1: Compare $P(A|B)$ with $P(A)$.
   From part (a), we found that $P(A|B)\approx 0.604$.
   We are given that $P(A)=0.73$.
   $$0.604\ne 0.73$$

   Since $P(A|B)\ne P(A)$, the events are not independent.

   Answer (c): A and B are not independent because $P(A|B)\ne P(A)$.

2. For two events A and B, P(A)=0.26, P(B)=0.37, and P(A∩B)=0.11.
   1. Find P(A|B).
   2. Find P(B|A).
   3. Determine whether or not A and B are independent.
   Answer (click to Show/Hide)

   This problem uses the formula for conditional probability and the definition of independent events.

   The formula for conditional probability of event A given event B is:
   $$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

   a. Find $P(A|B)$

   We substitute the given values into the formula.
   $$P(A|B)=\frac{0.11}{0.37}\approx 0.297$$

   Answer (a): $P(A|B)\approx 0.297$.

   b. Find $P(B|A)$

   We use the corresponding formula for $P(B|A)$.
   $$P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{0.11}{0.26}\approx 0.423$$

   Answer (b): $P(B|A)\approx 0.423$.

   c. Determine whether or not A and B are independent.

   Two events A and B are independent if $P(A|B)=P(A)$. We can use our result from part (a) to check if this condition is met.

   Step 1: Compare $P(A|B)$ with $P(A)$.
   From part (a), we found that $P(A|B)\approx 0.297$.
   We are given that $P(A)=0.26$.
   $$0.297\ne 0.26$$

   Since $P(A|B)\ne P(A)$, the events are not independent.

   Answer (c): A and B are not independent because $P(A|B)\ne P(A)$.

3. For two events A and B, P(A)=0.25, P(B)=0.6, and P(A∩B)=0.15.
   1. Find P(A|B).
   2. Find P(B|A).
   3. Determine whether or not A and B are independent.
   4. Determine whether or not A and B are mutually exclusive.
   Answer (click to Show/Hide)

   This problem uses the formulas for conditional probability, independent events, and mutually exclusive events.

   a. Find $P(A|B)$

   The formula for conditional probability is $P(A|B)=\frac{P(A\cap B)}{P(B)}$.
   We substitute the given values into the formula.
   $$P(A|B)=\frac{0.15}{0.6}=0.25$$

   Answer (a): $P(A|B)=0.25$.

   b. Find $P(B|A)$

   We use the corresponding formula for $P(B|A)$.
   $$P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{0.15}{0.25}=0.6$$

   Answer (b): $P(B|A)=0.6$.

   c. Determine whether or not A and B are independent.

   Two events A and B are independent if $P(A|B)=P(A)$.
   From part (a), we found that $P(A|B)=0.25$.
   We are given that $P(A)=0.25$.
   Since $0.25=0.25$, the events are independent.

   Answer (c): A and B are independent because $P(A|B)=P(A)$.

   d. Determine whether or not A and B are mutually exclusive.

   Two events are mutually exclusive if they cannot happen at the same time, which means their intersection is zero: $P(A\cap B)=0$.
   We are given that $P(A\cap B)=0.15$.
   Since $0.15\ne 0$, the events are not mutually exclusive.

   Answer (d): A and B are not mutually exclusive because their probability of occurring together is greater than 0.

4. Compute the following probabilities in connection with the roll of a single fair die.
   1. The probability that the roll is even.
   2. The probability that the roll is even, given that it is not a two.
   3. The probability that the roll is even, given that it is not a one.
   Answer (click to Show/Hide)

   The sample space for a single fair die roll is S = {1, 2, 3, 4, 5, 6}.

   a. The probability that the roll is even.

   This is a basic probability problem. The event E is “the roll is even.”

   Step 1: Find the number of favorable outcomes.
   The even numbers in the sample space are {2, 4, 6}. There are 3 favorable outcomes.

   Step 2: Calculate the probability.
   The total number of outcomes is 6.
   $$P(\text{Even})=\frac{\text{Number of even outcomes}}{\text{Total number of outcomes}}=\frac{3}{6}=\frac{1}{2}$$

   Answer (a): The probability of rolling an even number is 1/2.

   b. The probability that the roll is even, given that it is not a two.

   Let A be the event “the roll is even” and B be the event “the roll is not a two.” We want to find $P(A|B)$.

   The formal definition for conditional probability is: $$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

   Step 1: Find P(B), the probability the roll is not a two.
   The outcomes for “not a two” are {1, 3, 4, 5, 6}. There are 5 such outcomes.
   $$P(B)=P(Not\; a\; 2)=\frac{5}{6}$$

   Step 2: Find P(A∩B), the probability the roll is even AND not a two.
   The outcomes that are both even and not a two are {4, 6}. There are 2 such outcomes.
   $$P(A\cap B)=P(Even\; and\; Not\; a\; 2)=\frac{2}{6}$$

   Step 3: Calculate P(A|B).
   $$P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{2/6}{5/6}=\frac{2}{5}$$

   Alternative Method (Reduced Sample Space):
   The given condition, “the roll is not a two,” reduces our sample space to S’ = {1, 3, 4, 5, 6}. Within this new space of 5 outcomes, the favorable (even) outcomes are {4, 6}. There are 2 favorable outcomes. Therefore, the probability is 2/5.

   Answer (b): The probability is 2/5.

   c. The probability that the roll is even, given that it is not a one.

   Let A be the event “the roll is even” and C be the event “the roll is not a one.” We want to find $P(A|C)$.

   Step 1: Find P(C), the probability the roll is not a one.
   The outcomes for “not a one” are {2, 3, 4, 5, 6}. There are 5 such outcomes.
   $$P(C)=P(Not\; a\; 1)=\frac{5}{6}$$

   Step 2: Find P(A∩C), the probability the roll is even AND not a one.
   The outcomes that are both even and not a one are {2, 4, 6}. There are 3 such outcomes.
   $$P(A\cap C)=P(Even\; and\; Not\; a\; 1)=\frac{3}{6}$$

   Step 3: Calculate P(A|C).
   $$P(A|C)=\frac{P(A\cap C)}{P(C)}=\frac{3/6}{5/6}=\frac{3}{5}$$

   Alternative Method (Reduced Sample Space):
   The given condition, “the roll is not a one,” reduces our sample space to S” = {2, 3, 4, 5, 6}. Within this new space of 5 outcomes, the favorable (even) outcomes are {2, 4, 6}. There are 3 favorable outcomes. Therefore, the probability is 3/5.

   Answer (c): The probability is 3/5.

5. Compute the following probabilities in connection with two tosses of a fair coin.
   1. The probability that the second toss is heads.
   2. The probability that the second toss is heads, given that the first toss is heads.
   3. The probability that the second toss is heads, given that at least one of the two tosses is heads.
   Answer (click to Show/Hide)

   The sample space for two tosses of a fair coin is S = {HH, HT, TH, TT}, where H denotes heads and T denotes tails. There are 4 total equally likely outcomes.

   a. The probability that the second toss is heads.

   This is a basic probability problem. Let A be the event “the second toss is heads.”

   Step 1: Find the number of favorable outcomes.
   The outcomes where the second toss is heads are {HH, TH}. There are 2 favorable outcomes.

   Step 2: Calculate the probability.
   The total number of outcomes is 4.
   $$P(A)=\frac{\text{Number of outcomes with second toss H}}{\text{Total number of outcomes}}=\frac{2}{4}=\frac{1}{2}$$

   Answer (a): The probability that the second toss is heads is 1/2.

   b. The probability that the second toss is heads, given that the first toss is heads.

   Let A be the event “the second toss is heads” and B be the event “the first toss is heads.” We want to find $P(A|B)$.

   The formal definition for conditional probability is: $$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

   Step 1: Find P(B), the probability the first toss is heads.
   The outcomes for “first toss is heads” are {HH, HT}. There are 2 such outcomes.
   $$P(B)=\frac{2}{4}=\frac{1}{2}$$

   Step 2: Find P(A∩B), the probability the first toss is heads AND the second toss is heads.
   The only outcome that satisfies this is {HH}. There is 1 such outcome.
   $$P(A\cap B)=\frac{1}{4}$$

   Step 3: Calculate P(A|B).
   $$P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{1/4}{2/4}=\frac{1}{2}$$

   Alternative Method (Reduced Sample Space):
   The given condition, “the first toss is heads,” reduces our sample space to S’ = {HH, HT}. Within this new space of 2 outcomes, the favorable outcome (second toss is heads) is {HH}. There is 1 favorable outcome. Therefore, the probability is 1/2.

   Answer (b): The probability is 1/2.

   c. The probability that the second toss is heads, given that at least one of the two tosses is heads.

   Let A be the event “the second toss is heads” and C be the event “at least one toss is heads.” We want to find $P(A|C)$.

   Step 1: Find P(C), the probability at least one toss is heads.
   The outcomes for “at least one heads” are {HH, HT, TH}. There are 3 such outcomes.
   $$P(C)=\frac{3}{4}$$

   Step 2: Find P(A∩C), the probability the second toss is heads AND at least one toss is heads.
   The outcomes that satisfy both conditions are {HH, TH}. There are 2 such outcomes.
   $$P(A\cap C)=\frac{2}{4}$$

   Step 3: Calculate P(A|C).
   $$P(A|C)=\frac{P(A\cap C)}{P(C)}=\frac{2/4}{3/4}=\frac{2}{3}$$

   Alternative Method (Reduced Sample Space):
   The given condition, “at least one of the two tosses is heads,” reduces our sample space to S” = {HH, HT, TH}. Within this new space of 3 outcomes, the favorable outcomes (second toss is heads) are {HH, TH}. There are 2 favorable outcomes. Therefore, the probability is 2/3.

   Answer (c): The probability is 2/3.

6. A special deck of 16 cards has 4 that are blue, 4 yellow, 4 green, and 4 red. The four cards of each color are numbered from one to four. A single card is drawn at random. Find the following probabilities.
   1. The probability that the card drawn is red.
   2. The probability that the card is red, given that it is not green.
   3. The probability that the card is red, given that it is neither red nor yellow.
   4. The probability that the card is red, given that it is not a four.
   Answer (click to Show/Hide)

   The total sample space has 16 cards.

   a. The probability that the card drawn is red.
   There are 4 red cards out of 16 total cards.
   $$P(\text{Red})=\frac{4}{16}=\frac{1}{4}$$
   Answer (a): The probability is 1/4.

   b. The probability that the card is red, given that it is not green.
   The condition “not green” reduces the sample space to 12 cards (4 red, 4 blue, 4 yellow). Within this smaller group, there are 4 red cards.
   $$P(\text{Red}|\text{Not Green})=\frac{4}{12}=\frac{1}{3}$$
   Answer (b): The probability is 1/3.

   c. The probability that the card is red, given that it is neither red nor yellow.
   The condition “neither red nor yellow” reduces the sample space to the 8 cards that are blue or green. Within this group, there are 0 red cards.
   $$P(\text{Red}|\text{Neither Red nor Yellow})=\frac{0}{8}=0$$
   Answer (c): The probability is 0.

   d. The probability that the card is red, given that it is not a four.
   The condition “not a four” reduces the sample space to 12 cards (the cards numbered 1, 2, and 3 for each of the four colors). Within this group, there are 3 red cards (the red 1, red 2, and red 3).
   $$P(\text{Red}|\text{Not a Four})=\frac{3}{12}=\frac{1}{4}$$
   Answer (d): The probability is 1/4.

7. A special deck of 16 cards has 4 that are blue, 4 yellow, 4 green, and 4 red. The four cards of each color are numbered from one to four. A single card is drawn at random. Find the following probabilities.
   1. The probability that the card drawn is a two or a four.
   2. The probability that the card is a two or a four, given that it is not a one.
   3. The probability that the card is a two or a four, given that it is either a two or a three.
   4. The probability that the card is a two or a four, given that it is red or green.
   Answer (click to Show/Hide)

   The total sample space has 16 cards.

   a. The probability that the card drawn is a two or a four.
   There are 4 cards numbered “two” and 4 cards numbered “four,” for a total of 8 favorable outcomes out of 16 total cards.
   $$P(\text{Two or Four})=\frac{8}{16}=\frac{1}{2}$$
   Answer (a): The probability is 1/2.

   b. The probability that the card is a two or a four, given that it is not a one.
   The condition “not a one” reduces the sample space to 12 cards (all cards except the four “ones”). Within this group, there are still 4 “twos” and 4 “fours,” making 8 favorable outcomes.
   $$P(\text{Two or Four}|\text{Not a One})=\frac{8}{12}=\frac{2}{3}$$
   Answer (b): The probability is 2/3.

   c. The probability that the card is a two or a four, given that it is either a two or a three.
   The condition “either a two or a three” reduces the sample space to 8 cards (the four “twos” and the four “threes”). Within this group, only the 4 “twos” are favorable outcomes.
   $$P(\text{Two or Four}|\text{Two or Three})=\frac{4}{8}=\frac{1}{2}$$
   Answer (c): The probability is 1/2.

   d. The probability that the card is a two or a four, given that it is red or green.
   The condition “red or green” reduces the sample space to 8 cards (the 4 red and 4 green cards). Within this group, there are 2 favorable outcomes from the red cards (the red 2 and 4) and 2 from the green cards (the green 2 and 4), for a total of 4 favorable outcomes.
   $$P(\text{Two or Four}|\text{Red or Green})=\frac{4}{8}=\frac{1}{2}$$
   Answer (d): The probability is 1/2.

8. A random experiment gave rise to the two-way contingency table shown. Use it to compute the probabilities indicated.
   

   	R	S
   A	0.12	0.18
   B	0.28	0.42

   1. P(A), P(R), P(A∩R).
   2. Based on the answer to (a), determine whether or not the events A and R are independent.
   3. Based on the answer to (b), determine whether or not P(A|R) can be predicted without any computation. If so, make the prediction. In any case, compute P(A|R) using the Rule for Conditional Probability.
   Answer (click to Show/Hide)

   First, it’s helpful to add totals to the contingency table.

   	R	S	Row Total
   A	0.12	0.18	0.30
   B	0.28	0.42	0.70
   Column Total	0.40	0.60	1.00

   a. Find P(A), P(R), P(A∩R).

   $P(A)$ is the total probability for row A, which is the sum of the probabilities in that row.
   $$P(A)=0.12+0.18=0.30$$

   $P(R)$ is the total probability for column R, which is the sum of the probabilities in that column.
   $$P(R)=0.12+0.28=0.40$$

   $P(A\cap R)$ is the probability of the intersection of A and R, which is the value in the cell where they meet.
   $$P(A\cap R)=0.12$$

   Answer (a): $P(A)=0.30$, $P(R)=0.40$, and $P(A\cap R)=0.12$.

   b. Based on the answer to (a), determine whether or not the events A and R are independent.

   Two events are independent if $P(A\cap R)=P(A)\times P(R)$. Let’s check this condition.
   $$P(A)\times P(R)=0.30\times 0.40=0.12$$
   We found that $P(A\cap R)$ is also 0.12. Since the values are equal, the events are independent.

   Answer (b): The events A and R are independent.

   c. Based on the answer to (b), determine whether or not P(A|R) can be predicted without any computation.

   Yes, it can be predicted. Because we found that A and R are independent events, we know that the occurrence of R does not affect the probability of A. Therefore, $P(A|R)$ must be equal to $P(A)$. The prediction is that $P(A|R)=0.30$.

   Now we compute it using the rule for conditional probability to confirm:
   $$P(A|R)=\frac{P(A\cap R)}{P(R)}=\frac{0.12}{0.40}=0.30$$
   The computation matches the prediction.

   Answer (c): Yes, it can be predicted to be 0.30. The computation confirms this result.

9. A random experiment gave rise to the two-way contingency table shown. Use it to compute the probabilities indicated.
   

   	R	S
   A	0.13	0.07
   B	0.61	0.19

   1. P(A), P(R), P(A∩R).
   2. Based on the answer to (a), determine whether or not the events A and R are independent.
   3. Based on the answer to (b), determine whether or not P(A|R) can be predicted without any computation. If so, make the prediction. In any case, compute P(A|R) using the Rule for Conditional Probability.
   Answer (click to Show/Hide)

   First, it’s helpful to add totals to the contingency table.

   	R	S	Row Total
   A	0.13	0.07	0.20
   B	0.61	0.19	0.80
   Column Total	0.74	0.26	1.00

   a. Find P(A), P(R), P(A∩R).

   $P(A)$ is the total probability for row A.
   $$P(A)=0.13+0.07=0.20$$

   $P(R)$ is the total probability for column R.
   $$P(R)=0.13+0.61=0.74$$

   $P(A\cap R)$ is the value in the cell where A and R intersect.
   $$P(A\cap R)=0.13$$

   Answer (a): $P(A)=0.20$, $P(R)=0.74$, and $P(A\cap R)=0.13$.

   b. Based on the answer to (a), determine whether or not the events A and R are independent.

   Two events are independent if $P(A\cap R)=P(A)\times P(R)$. Let’s check this condition.
   $$P(A)\times P(R)=0.20\times 0.74=0.148$$
   We found that $P(A\cap R)$ is 0.13. Since $0.13\ne 0.148$, the events are not independent.

   Answer (b): The events A and R are not independent.

   c. Based on the answer to (b), determine whether or not P(A|R) can be predicted without any computation.

   No, it cannot be predicted. Because the events A and R are not independent, the probability of A is affected by the occurrence of R. Therefore, $P(A|R)$ will not be equal to $P(A)$.

   We must compute it using the rule for conditional probability:
   $$P(A|R)=\frac{P(A\cap R)}{P(R)}=\frac{0.13}{0.74}\approx 0.176$$

   Answer (c): No, it cannot be predicted. The computed value is approximately 0.176.

10. Suppose for events A and B in a random experiment P(A)=0.70 and P(B)=0.30. Compute the indicated probability, or explain why there is not enough information to do so.
    1. P(A∩B).
    2. P(A∩B), with the extra information that A and B are independent.
    3. P(A∩B), with the extra information that A and B are mutually exclusive.
    Answer (click to Show/Hide)

    a. P(A∩B).

    With only the probabilities of the individual events, $P(A)$ and $P(B)$, it is impossible to compute the probability of their intersection, $P(A\cap B)$. We do not know if the events are independent, mutually exclusive, or have some other relationship.

    Answer (a): There is not enough information to compute the probability.

    b. P(A∩B), with the extra information that A and B are independent.

    If events A and B are independent, then the probability of their intersection is the product of their individual probabilities.
    $$P(A\cap B)=P(A)\times P(B)$$

    Step 1: Substitute the given values.
    $$P(A\cap B)=0.70\times 0.30=0.21$$

    Answer (b): If A and B are independent, $P(A\cap B)=0.21$.

    c. P(A∩B), with the extra information that A and B are mutually exclusive.

    If two events are mutually exclusive, they cannot both occur at the same time. This means their intersection is empty, and the probability of their intersection is zero.
    $$P(A\cap B)=0$$

    Answer (c): If A and B are mutually exclusive, $P(A\cap B)=0$.

11. Suppose for events A and B connected to some random experiment, P(A)=0.50 and P(B)=0.50. Compute the indicated probability, or explain why there is not enough information to do so.
    1. P(A∩B).
    2. P(A∩B), with the extra information that A and B are independent.
    3. P(A∩B), with the extra information that A and B are mutually exclusive.
    Answer (click to Show/Hide)

    a. P(A∩B).

    With only the probabilities of the individual events, $P(A)$ and $P(B)$, it is impossible to compute the probability of their intersection, $P(A\cap B)$. We do not know if the events are independent, mutually exclusive, or have some other relationship.

    Answer (a): There is not enough information to compute the probability.

    b. P(A∩B), with the extra information that A and B are independent.

    If events A and B are independent, then the probability of their intersection is the product of their individual probabilities.
    $$P(A\cap B)=P(A)\times P(B)$$

    Step 1: Substitute the given values.
    $$P(A\cap B)=0.50\times 0.50=0.25$$

    Answer (b): If A and B are independent, $P(A\cap B)=0.25$.

    c. P(A∩B), with the extra information that A and B are mutually exclusive.

    If two events are mutually exclusive, they cannot both occur at the same time. This means their intersection is empty, and the probability of their intersection is zero.
    $$P(A\cap B)=0$$

    Answer (c): If A and B are mutually exclusive, $P(A\cap B)=0$.

12. The following two-way contingency table gives the breakdown of the population of patrons at a grocery store according to the number of items purchased and whether or not the patron made an impulse purchase at the checkout counter:
    

    Number of Items	Impulse Purchase
    	Made	Not Made
    Few	0.01	0.19
    Many	0.04	0.76

    A patron is selected at random. Find each of the following probabilities.

    1. The patron made an impulse purchase.
    2. The patron made an impulse purchase, given that the total number of items purchased was many.
    3. Determine whether or not the events “few purchases” and “made an impulse purchase at the checkout counter” are independent.
    Answer (click to Show/Hide)

    First, we create a new table with row and column totals, which will help in our calculations. Let F be the event “few items,” M be the event “many items,” I be the event “made impulse purchase,” and N be the event “no impulse purchase.”

    	I (Made)	N (Not Made)	Row Total
    F (Few)	0.01	0.19	0.20
    M (Many)	0.04	0.76	0.80
    Column Total	0.05	0.95	1.00

    a. The patron made an impulse purchase.

    This corresponds to the total probability of the “Made” column.
    $$P(I)=0.01+0.04=0.05$$

    Answer (a): The probability that a patron made an impulse purchase is 0.05.

    b. The patron made an impulse purchase, given that the total number of items purchased was many.

    This is the conditional probability $P(I|M)$. We use the formula:
    $$P(I|M)=\frac{P(I\cap M)}{P(M)}$$
    From the table, $P(I\cap M)=0.04$ and $P(M)=0.80$.
    $$P(I|M)=\frac{0.04}{0.80}=0.05$$

    Answer (b): The probability is 0.05.

    c. Determine whether or not the events “few purchases” and “made an impulse purchase at the checkout counter” are independent.

    The events F (“few purchases”) and I (“made an impulse purchase”) are independent if $P(F\cap I)=P(F)\times P(I)$.

    Step 1: Find the probabilities from the table.

    $P(F\cap I)=0.01$

    $P(F)=0.20$

    $P(I)=0.05$

    Step 2: Check if the condition for independence is met.
    $$P(F)\times P(I)=0.20\times 0.05=0.01$$
    Since $P(F\cap I)$ is also 0.01, the condition is met.

    Answer (c): The events are independent.

13. The sensitivity of a drug test, also known as its true positive rate, is the probability that the test correctly returns a positive result for a person who has actually taken the drug. Suppose that there are two independent tests to detect the presence of a certain type of banned drugs in athletes. One has sensitivity 0.75; the other has sensitivity 0.85. If both are applied to an athlete who has taken this type of drug, what is the chance that their usage will go undetected?
    
    Answer (click to Show/Hide)

    Let T1 be the event that the first test is positive, and T2 be the event that the second test is positive. The sensitivities are given as probabilities:
    $$P(\mathrm{T1})=0.75$$
    $$P(\mathrm{T2})=0.85$$

    The drug usage will go undetected if both tests are negative. Let T1^C and T2^C be the events that the first and second tests are negative, respectively. These are the complements of T1 and T2.

    Step 1: Find the probability of each test being negative.
    The probability of a complement event is 1 minus the probability of the event.
    $$P({\mathrm{T1}}^C)=1-P(\mathrm{T1})=1-0.75=0.25$$
    $$P({\mathrm{T2}}^C)=1-P(\mathrm{T2})=1-0.85=0.15$$

    Step 2: Find the probability of both tests being negative.
    Since the two tests are independent, the events T1^C and T2^C are also independent. The probability that both events occur is the product of their individual probabilities.
    $$P({\mathrm{T1}}^C\cap {\mathrm{T2}}^C)=P({\mathrm{T1}}^C)\times P({\mathrm{T2}}^C)=0.25\times 0.15=0.0375$$

    Answer: The chance that the drug usage will go undetected is 0.0375, or 3.75%.

14. A person has two lights in their well house to keep the pipes from freezing in winter. They check the lights daily. Each light has probability 0.002 of burning out before it is checked the next day (independently of the other light).
    1. If the lights are wired in parallel one will continue to shine even if the other burns out. In this situation, compute the probability that at least one light will continue to shine for the full 24 hours. Note the greatly increased reliability of the system of two bulbs over that of a single bulb.
    2. If the lights are wired in series neither one will continue to shine even if only one of them burns out. In this situation, compute the probability that at least one light will continue to shine for the full 24 hours. Note the slightly decreased reliability of the system of two bulbs over that of a single bulb.
    Answer (click to Show/Hide)

    Let B1 be the event that the first light burns out, and B2 be the event that the second light burns out. We are given the probabilities:
    $$P(\mathrm{B1})=0.002$$
    $$P(\mathrm{B2})=0.002$$

    a. Lights Wired in Parallel

    The event “at least one light will continue to shine” is the complement of the event “both lights burn out.” Let’s find the probability that both lights burn out and subtract it from 1.

    Step 1: Find the probability of both lights burning out.
    Since the events are independent, the probability that both B1 and B2 occur is the product of their individual probabilities.
    $$P(\mathrm{B1}\cap \mathrm{B2})=P(\mathrm{B1})\times P(\mathrm{B2})=0.002\times 0.002=0.000004$$

    Step 2: Use the complement rule.
    The probability of the complement event, “at least one light shines,” is 1 minus the probability that both burn out.
    $$P(\text{at least one shines})=1-P(\mathrm{B1}\cap \mathrm{B2})=1-0.000004=0.999996$$

    Answer (a): The probability that at least one light will continue to shine is 0.999996, or 99.9996%.

    b. Lights Wired in Series

    If the lights are in series, the system only works if both lights continue to shine. Let B1^C and B2^C be the events that the first and second lights continue to shine, respectively.

    Step 1: Find the probability of each light continuing to shine.
    This is the complement of the probability that a light burns out.
    $$P({\mathrm{B1}}^C)=1-P(\mathrm{B1})=1-0.002=0.998$$
    $$P({\mathrm{B2}}^C)=1-P(\mathrm{B2})=1-0.002=0.998$$

    Step 2: Find the probability of both lights continuing to shine.
    Since the events are independent, the probability that both B1^C and B2^C occur is the product of their individual probabilities.
    $$P({\mathrm{B1}}^C\cap {\mathrm{B2}}^C)=P({\mathrm{B1}}^C)\times P({\mathrm{B2}}^C)=0.998\times 0.998=0.996004$$

    Answer (b): The probability that at least one light will continue to shine (which means both must shine) is 0.996004, or 99.6004%.

15. Events A and B are mutually exclusive. Find P(A|B).
    
    Answer (click to Show/Hide)

    This problem requires understanding the definitions of mutually exclusive events and conditional probability.

    Step 1: Understand Mutually Exclusive Events.
    If two events, A and B, are mutually exclusive, it means that they cannot both happen at the same time. The occurrence of one event precludes the occurrence of the other. Mathematically, this means the probability of their intersection is zero.
    $$P(A\cap B)=0$$

    Step 2: Use the Conditional Probability Formula.
    The formula for the conditional probability of A given B is:
    $$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

    Step 3: Substitute and Solve.
    We substitute the value from Step 1 into the formula from Step 2.
    $$P(A|B)=\frac{0}{P(B)}=0$$

    This makes intuitive sense: if we know that event B has occurred, then it is impossible for event A to have occurred, since they are mutually exclusive.

    Answer: The probability P(A|B) is 0.

16. A basketball player makes 60% of the free throws that he attempts, except that if he has just tried and missed a free throw then his chances of making a second one go down to only 30%. Suppose he has just been awarded two free throws.
    1. Find the probability that he makes both.
    2. Find the probability that he makes at least one.
    Answer (click to Show/Hide)

    Let M1 be the event that the player makes the first free throw, and M2 be the event that he makes the second. Let M1^C and M2^C be the corresponding events that he misses the shots.

    From the problem statement, we can define the following probabilities:

    The probability of making the first shot is $P(\mathrm{M1})=0.60$.

    The probability of missing the first shot is $P({\mathrm{M1}}^C)=1-0.60=0.40$.

    The probability of making the second shot, given he missed the first, is $P(\mathrm{M2}|{\mathrm{M1}}^C)=0.30$.

    Since the probability only changes after a miss, the probability of making the second shot, given he made the first, remains unchanged: $P(\mathrm{M2}|\mathrm{M1})=0.60$.

    a. Find the probability that he makes both.

    This is the probability that he makes the first shot AND makes the second shot, $P(\mathrm{M1}\cap \mathrm{M2})$. We use the multiplication rule for conditional probability.
    $$P(\mathrm{M1}\cap \mathrm{M2})=P(\mathrm{M1})\times P(\mathrm{M2}|\mathrm{M1})$$
    $$P(\mathrm{M1}\cap \mathrm{M2})=0.60\times 0.60=0.36$$

    Answer (a): The probability that he makes both free throws is 0.36.

    b. Find the probability that he makes at least one.

    The event “he makes at least one” is the complement of the event “he misses both.” It is easier to calculate the probability that he misses both shots and subtract this from 1.

    Step 1: Find the probability that he misses both shots.
    This is the probability he misses the first shot AND misses the second shot, $P({\mathrm{M1}}^C\cap {\mathrm{M2}}^C)$.
    First, we need the probability of missing the second shot, given he missed the first:
    $$P({\mathrm{M2}}^C|{\mathrm{M1}}^C)=1-P(\mathrm{M2}|{\mathrm{M1}}^C)=1-0.30=0.70$$
    Now we can find the probability of missing both:
    $$P({\mathrm{M1}}^C\cap {\mathrm{M2}}^C)=P({\mathrm{M1}}^C)\times P({\mathrm{M2}}^C|{\mathrm{M1}}^C)=0.40\times 0.70=0.28$$

    Step 2: Use the complement rule.
    The probability of making at least one shot is 1 minus the probability of missing both.
    $$P(\text{at least one made})=1-P({\mathrm{M1}}^C\cap {\mathrm{M2}}^C)=1-0.28=0.72$$

    Answer (b): The probability that he makes at least one free throw is 0.72.

17. Suppose a jar contains 17 red marbles and 32 blue marbles. If you reach in the jar and pull out 2 marbles at random one at a time without replacement, find the probability that both are red.
    
    Answer (click to Show/Hide)

    This is a conditional probability problem because the outcome of the second draw is dependent on the outcome of the first draw (since the marble is not replaced).

    Let R1 be the event that the first marble drawn is red, and R2 be the event that the second marble drawn is red. We want to find the probability that the first is red AND the second is red, which can be written as $P(\mathrm{R1}\cap \mathrm{R2})$.

    We use the multiplication rule for conditional probability:
    $$P(\mathrm{R1}\cap \mathrm{R2})=P(\mathrm{R1})\times P(\mathrm{R2}|\mathrm{R1})$$

    Step 1: Find the probability that the first marble is red.
    Initially, there are 17 red marbles and a total of 17 + 32 = 49 marbles.
    $$P(\mathrm{R1})=\frac{17}{49}$$

    Step 2: Find the probability that the second marble is red, given the first was red.
    After drawing one red marble, there are 16 red marbles remaining and a total of 48 marbles left in the jar.
    $$P(\mathrm{R2}|\mathrm{R1})=\frac{16}{48}=\frac{1}{3}$$

    Step 3: Calculate the probability of both events occurring.
    Now we multiply the probabilities from the first two steps.
    $$P(\mathrm{R1}\cap \mathrm{R2})=\frac{17}{49}\times \frac{16}{48}=\frac{17}{49}\times \frac{1}{3}=\frac{17}{147}$$
    As a decimal, this is approximately 0.1156.

    Answer: The probability that both marbles are red is 17/147, or about 11.6%.

18. Suppose you write each letter of the alphabet on a different slip of paper and put the slips into a hat. If you pull out two slips at random (one at a time without replacement), find the probability that both are vowels (a, e, i, o , or u).
    
    Answer (click to Show/Hide)

    This is a conditional probability problem because the outcome of the second draw is dependent on the outcome of the first draw (since the slip is not replaced).

    Let V1 be the event that the first slip drawn is a vowel, and V2 be the event that the second slip drawn is a vowel. We want to find the probability that the first is a vowel AND the second is a vowel, which is $P(\mathrm{V1}\cap \mathrm{V2})$.

    We use the multiplication rule for conditional probability:
    $$P(\mathrm{V1}\cap \mathrm{V2})=P(\mathrm{V1})\times P(\mathrm{V2}|\mathrm{V1})$$

    Step 1: Find the probability that the first slip is a vowel.
    There are 26 letters in total and 5 of them are vowels.
    $$P(\mathrm{V1})=\frac{5}{26}$$

    Step 2: Find the probability that the second slip is a vowel, given the first was a vowel.
    After drawing one vowel, there are 4 vowels remaining and a total of 25 slips left in the hat.
    $$P(\mathrm{V2}|\mathrm{V1})=\frac{4}{25}$$

    Step 3: Calculate the probability of both events occurring.
    Now we multiply the probabilities from the first two steps.
    $$P(\mathrm{V1}\cap \mathrm{V2})=\frac{5}{26}\times \frac{4}{25}=\frac{20}{650}=\frac{2}{65}$$
    As a decimal, this is approximately 0.0308.

    Answer: The probability that both slips are vowels is 2/65, or about 3.1%.

19. A math class consists of 25 students, 14 female and 11 male.  Two students are selected at random to participate in a probability experiment.  Compute the probability that
    1. a male is selected, then a female.
    2. a female is selected, then a male.
    3. two males are selected.
    4. two females are selected.
    5. no males are selected.
    Answer (click to Show/Hide)

    This problem involves conditional probability as the students are selected without replacement. The total number of students is 25.

    a. A male is selected, then a female.

    Let M1 be the event “the first student is male” and F2 be the event “the second student is female.”

    The probability of selecting a male first is $P(\mathrm{M1})=\frac{11}{25}$.

    After a male is chosen, there are 24 students left, 14 of whom are female. The probability of selecting a female second is $P(\mathrm{F2}|\mathrm{M1})=\frac{14}{24}$.
    $$P(\mathrm{M1}\cap \mathrm{F2})=\frac{11}{25}\times \frac{14}{24}=\frac{154}{600}=\frac{77}{300}$$
    Answer (a): The probability is 77/300.

    b. A female is selected, then a male.

    Let F1 be the event “the first student is female” and M2 be the event “the second student is male.”

    The probability of selecting a female first is $P(\mathrm{F1})=\frac{14}{25}$.

    After a female is chosen, there are 24 students left, 11 of whom are male. The probability of selecting a male second is $P(\mathrm{M2}|\mathrm{F1})=\frac{11}{24}$.
    $$P(\mathrm{F1}\cap \mathrm{M2})=\frac{14}{25}\times \frac{11}{24}=\frac{154}{600}=\frac{77}{300}$$
    Answer (b): The probability is 77/300.

    c. Two males are selected.

    The probability of selecting a male first is $P(\mathrm{M1})=\frac{11}{25}$.

    After a male is chosen, there are 10 males left out of 24 students. The probability of selecting another male is $P(\mathrm{M2}|\mathrm{M1})=\frac{10}{24}$.
    $$P(\mathrm{M1}\cap \mathrm{M2})=\frac{11}{25}\times \frac{10}{24}=\frac{110}{600}=\frac{11}{60}$$
    Answer (c): The probability is 11/60.

    d. Two females are selected.

    The probability of selecting a female first is $P(\mathrm{F1})=\frac{14}{25}$.

    After a female is chosen, there are 13 females left out of 24 students. The probability of selecting another female is $P(\mathrm{F2}|\mathrm{F1})=\frac{13}{24}$.
    $$P(\mathrm{F1}\cap \mathrm{F2})=\frac{14}{25}\times \frac{13}{24}=\frac{182}{600}=\frac{91}{300}$$
    Answer (d): The probability is 91/300.

    e. No males are selected.
    This event is identical to the event “two females are selected.”
    Answer (e): The probability is 91/300.

20. A math class consists of 25 students, 14 female and 11 male.  Three students are selected at random to participate in a probability experiment.  Compute the probability that
    1. a male is selected, then two females.
    2. a female is selected, then two males.
    3. two females are selected, then one male.
    4. three males are selected.
    5. three females are selected.
    Answer (click to Show/Hide)

    This problem involves conditional probability as the students are selected without replacement from a total of 25 students.

    a. A male is selected, then two females (M, F, F).
    $$P(\text{M, F, F})=\frac{11}{25}\times \frac{14}{24}\times \frac{13}{23}=\frac{2002}{13800}=\frac{1001}{6900}$$
    Answer (a): The probability is 1001/6900.

    b. A female is selected, then two males (F, M, M).
    $$P(\text{F, M, M})=\frac{14}{25}\times \frac{11}{24}\times \frac{10}{23}=\frac{1540}{13800}=\frac{77}{690}$$
    Answer (b): The probability is 77/690.

    c. Two females are selected, then one male (F, F, M).
    $$P(\text{F, F, M})=\frac{14}{25}\times \frac{13}{24}\times \frac{11}{23}=\frac{2002}{13800}=\frac{1001}{6900}$$
    Answer (c): The probability is 1001/6900.

    d. Three males are selected (M, M, M).
    $$P(\text{M, M, M})=\frac{11}{25}\times \frac{10}{24}\times \frac{9}{23}=\frac{990}{13800}=\frac{33}{460}$$
    Answer (d): The probability is 33/460.

    e. Three females are selected (F, F, F).
    $$P(\text{F, F, F})=\frac{14}{25}\times \frac{13}{24}\times \frac{12}{23}=\frac{2184}{13800}=\frac{91}{575}$$
    Answer (e): The probability is 91/575.

21. A jar contains 6 red marbles numbered 1 to 6 and 8 blue marbles numbered 1 to 8. A marble is drawn at random from the jar. Find the probability the marble is red or odd-numbered.
    
    Answer (click to Show/Hide)

    This problem involves the union of two events. Let R be the event that the marble drawn is red, and let O be the event that the marble is odd-numbered. We want to find $P(R\cup O)$.

    The formula for the union of two events is:
    $$P(R\cup O)=P(R)+P(O)-P(R\cap O)$$

    Step 1: Find the total number of outcomes.
    There are 6 red + 8 blue = 14 marbles in the jar.

    Step 2: Find the probability of drawing a red marble, P(R).
    There are 6 red marbles.
    $$P(R)=\frac{6}{14}$$

    Step 3: Find the probability of drawing an odd-numbered marble, P(O).

    Odd-numbered red marbles: {1, 3, 5} (3 marbles)

    Odd-numbered blue marbles: {1, 3, 5, 7} (4 marbles)
    There are a total of 3 + 4 = 7 odd-numbered marbles.
    $$P(O)=\frac{7}{14}$$

    Step 4: Find the probability of drawing a marble that is both red and odd-numbered, P(R∩O).
    The red marbles with odd numbers are {1, 3, 5}. There are 3 such marbles.
    $$P(R\cap O)=\frac{3}{14}$$

    Step 5: Calculate the final probability.
    Now we use the union formula.
    $$P(R\cup O)=\frac{6}{14}+\frac{7}{14}-\frac{3}{14}=\frac{10}{14}=\frac{5}{7}$$

    Answer: The probability of drawing a marble that is red or odd-numbered is 5/7.

22. A jar contains 4 red marbles numbered 1 to 4 and 10 blue marbles numbered 1 to 10. A marble is drawn at random from the jar. Find the probability the marble is blue or even-numbered.
    
    Answer (click to Show/Hide)

    This problem involves the union of two events. Let B be the event that the marble drawn is blue, and let E be the event that the marble is even-numbered. We want to find $P(B\cup E)$.

    The formula for the union of two events is:
    $$P(B\cup E)=P(B)+P(E)-P(B\cap E)$$

    Step 1: Find the total number of outcomes.
    There are 4 red + 10 blue = 14 marbles in the jar.

    Step 2: Find the probability of drawing a blue marble, P(B).
    There are 10 blue marbles.
    $$P(B)=\frac{10}{14}$$

    Step 3: Find the probability of drawing an even-numbered marble, P(E).

    Even-numbered red marbles: {2, 4} (2 marbles)

    Even-numbered blue marbles: {2, 4, 6, 8, 10} (5 marbles)
    There are a total of 2 + 5 = 7 even-numbered marbles.
    $$P(E)=\frac{7}{14}$$

    Step 4: Find the probability of drawing a marble that is both blue and even-numbered, P(B∩E).
    The blue marbles with even numbers are {2, 4, 6, 8, 10}. There are 5 such marbles.
    $$P(B\cap E)=\frac{5}{14}$$

    Step 5: Calculate the final probability.
    Now we use the union formula.
    $$P(B\cup E)=\frac{10}{14}+\frac{7}{14}-\frac{5}{14}=\frac{12}{14}=\frac{6}{7}$$

    Answer: The probability of drawing a marble that is blue or even-numbered is 6/7.

23. A jar contains 5 red marbles numbered 1 to 5 and 8 blue marbles numbered 1 to 8. A marble is drawn at random from the jar. Find the probability the marble is
    1. Even-numbered given that the marble is red.
    2. Red given that the marble is even-numbered.
    Answer (click to Show/Hide)

    This problem involves conditional probability, where we find the probability of an event given that another event has already occurred. The total number of marbles in the jar is 5 + 8 = 13.

    a. Even-numbered given that the marble is red.

    Let E be the event “the marble is even-numbered” and R be the event “the marble is red.” We want to find $P(E|R)$.

    We can solve this by considering the reduced sample space. The condition “the marble is red” means we only need to consider the 5 red marbles.

    Step 1: Identify the new sample space.
    The sample space is the set of red marbles: {R1, R2, R3, R4, R5}. The total number of outcomes in this new space is 5.

    Step 2: Find the number of favorable outcomes within the new sample space.
    The favorable outcomes are the even-numbered marbles within the red marbles, which are {R2, R4}. There are 2 favorable outcomes.

    Step 3: Calculate the probability.
    $$P(E|R)=\frac{\text{Number of even red marbles}}{\text{Total number of red marbles}}=\frac{2}{5}$$

    Answer (a): The probability is 2/5.

    b. Red given that the marble is even-numbered.

    The condition “the marble is even-numbered” reduces our sample space.

    Step 1: Identify the new sample space.
    The even-numbered marbles are:

    Red: {R2, R4} (2 marbles)

    Blue: {B2, B4, B6, B8} (4 marbles)
    The new sample space is all even-numbered marbles, so the total number of outcomes is 2 + 4 = 6.

    Step 2: Find the number of favorable outcomes within the new sample space.
    The favorable outcomes are the red marbles within this group of even-numbered marbles, which are {R2, R4}. There are 2 favorable outcomes.

    Step 3: Calculate the probability.
    $$P(R|E)=\frac{\text{Number of red even marbles}}{\text{Total number of even marbles}}=\frac{2}{6}=\frac{1}{3}$$

    Answer (b): The probability is 1/3.

24. A jar contains 4 red marbles numbered 1 to 4 and 8 blue marbles numbered 1 to 8. A marble is drawn at random from the jar. Find the probability the marble is
    1. Odd-numbered given that the marble is blue.
    2. Blue given that the marble is odd-numbered.
    Answer (click to Show/Hide)

    This problem involves conditional probability. The total number of marbles in the jar is 4 + 8 = 12.

    a. Odd-numbered given that the marble is blue.

    Let O be the event “the marble is odd-numbered” and B be the event “the marble is blue.” We want to find $P(O|B)$.

    We can solve this by considering the reduced sample space. The condition “the marble is blue” means we only need to consider the 8 blue marbles.

    Step 1: Identify the new sample space.
    The sample space is the set of blue marbles: {B1, B2, B3, B4, B5, B6, B7, B8}. The total number of outcomes in this new space is 8.

    Step 2: Find the number of favorable outcomes within the new sample space.
    The favorable outcomes are the odd-numbered marbles within the blue marbles, which are {B1, B3, B5, B7}. There are 4 favorable outcomes.

    Step 3: Calculate the probability.
    $$P(O|B)=\frac{\text{Number of odd blue marbles}}{\text{Total number of blue marbles}}=\frac{4}{8}=\frac{1}{2}$$

    Answer (a): The probability is 1/2.

    b. Blue given that the marble is odd-numbered.

    Let B be the event “the marble is blue” and O be the event “the marble is odd-numbered.” We want to find $P(B|O)$.

    The condition “the marble is odd-numbered” reduces our sample space.

    Step 1: Identify the new sample space.
    The odd-numbered marbles are:

    Red: {R1, R3} (2 marbles)

    Blue: {B1, B3, B5, B7} (4 marbles)
    The new sample space is all odd-numbered marbles, so the total number of outcomes is 2 + 4 = 6.

    Step 2: Find the number of favorable outcomes within the new sample space.
    The favorable outcomes are the blue marbles within this group of odd-numbered marbles. There are 4 favorable outcomes.

    Step 3: Calculate the probability.
    $$P(B|O)=\frac{\text{Number of blue odd marbles}}{\text{Total number of odd marbles}}=\frac{4}{6}=\frac{2}{3}$$

    Answer (b): The probability is 2/3.

25. Compute the probability of flipping a fair coin and getting heads, given that the previous flip was tails.
    
    Answer (click to Show/Hide)

    To solve this formally, we will define the sample space for two consecutive coin flips and use the definition of conditional probability.

    Let H be heads and T be tails. The sample space S for two flips has four equally likely outcomes:
    S = {HH, HT, TH, TT}

    Let A be the event that the second toss is heads, and B be the event that the first toss is tails. We want to find the conditional probability $P(A|B)$.

    The formula for conditional probability is:
    $$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

    Step 1: Find the probability of event B (the first toss is tails).
    The outcomes where the first toss is tails are {TH, TT}. There are 2 such outcomes out of 4 total.
    $$P(B)=\frac{2}{4}=\frac{1}{2}$$

    Step 2: Find the probability of the intersection of A and B (the first toss is tails AND the second is heads).
    The only outcome that satisfies both conditions is {TH}. There is 1 such outcome out of 4 total.
    $$P(A\cap B)=\frac{1}{4}$$

    Step 3: Calculate the conditional probability.
    Now we substitute the values from the previous steps into the formula.
    $$P(A|B)=\frac{1/4}{2/4}=\frac{1}{2}$$

    This confirms that the outcome of the previous flip does not affect the outcome of the current flip, which is the definition of independence.

    Answer: The probability of getting heads is 1/2.

26. Find the probability of rolling a “1” on a fair die, given that the last 3 rolls were all ones.
    
    Answer (click to Show/Hide)

    This problem involves independent events. The outcome of one roll of a fair die has no effect on the outcome of any subsequent rolls. Each roll is a separate, independent event.

    Let A be the event “the current roll is a 1,” and let B be the event “the last 3 rolls were all ones.” We want to find the conditional probability $P(A|B)$.

    Step 1: Understand Independent Events.
    Two events are independent if the occurrence of one does not affect the probability of the other. For independent events, the following is true:
    $$P(A|B)=P(A)$$
    The information that the last 3 rolls were all ones is irrelevant to the outcome of the current roll.

    Step 2: Calculate the probability of rolling a “1”.
    For a single, fair six-sided die, there are six equally likely outcomes {1, 2, 3, 4, 5, 6}. The probability of rolling a “1” is:
    $$P(A)=\frac{1}{6}$$

    Because the events are independent, the condition that the previous three rolls were ones does not change this probability.

    Answer: The probability of rolling a “1” given that the last 3 rolls were a one is 1/6.

27. Suppose a math class contains 25 students, 14 females (three of whom speak French) and 11 males (two of whom speak French). Compute the probability that a randomly selected student speaks French, given that the student is female.
    
    Answer (click to Show/Hide)

    This is a conditional probability problem. We are given a condition—that the selected student is female—which reduces our total sample space.

    Let S be the event “the student speaks French,” and let F be the event “the student is female.” We want to find the probability $P(S|F)$.

    Step 1: Determine the reduced sample space.
    The condition “given that the student is female” means we are only considering the 14 female students as our possible outcomes.

    Total outcomes in the new sample space = 14.

    Step 2: Determine the number of favorable outcomes within the new sample space.
    A favorable outcome is a student who speaks French. The problem states that within the group of 14 females, three speak French.

    Number of favorable outcomes = 3.

    Step 3: Calculate the probability.
    The probability is the ratio of the favorable outcomes to the total outcomes in our reduced sample space.
    $$P(\text{Speaks French}|\text{Is Female})=\frac{\text{Number of females who speak French}}{\text{Total number of females}}=\frac{3}{14}$$

    Answer: The probability that a randomly selected student speaks French, given that the student is female, is 3/14.

28. Suppose a math class contains 25 students, 14 females (three of whom speak French) and 11 males (two of whom speak French). Compute the probability that a randomly selected student is male, given that the student speaks French.
    
    Answer (click to Show/Hide)

    This is a conditional probability problem. We are given a condition—that the selected student speaks French—which reduces our total sample space.

    Let M be the event “the student is male,” and let S be the event “the student speaks French.” We want to find the probability $P(M|S)$.

    Step 1: Determine the reduced sample space.
    The condition “given that the student speaks French” means we are only considering the students who speak French as our possible outcomes.

    Number of females who speak French = 3

    Number of males who speak French = 2
    The total number of students who speak French is 3 + 2 = 5.

    Total outcomes in the new sample space = 5.

    Step 2: Determine the number of favorable outcomes within the new sample space.
    A favorable outcome is a student who is male. The problem states that within the group of French speakers, two are male.

    Number of favorable outcomes = 2.

    Step 3: Calculate the probability.
    The probability is the ratio of the favorable outcomes to the total outcomes in our reduced sample space.
    $$P(\text{Is Male}|\text{Speaks French})=\frac{\text{Number of males who speak French}}{\text{Total number of students who speak French}}=\frac{2}{5}$$

    Answer: The probability that a randomly selected student is male, given that the student speaks French, is 2/5.

29. Consider the population of all undergraduates at a large university. Within this population, 48% are male and 18% are majoring in business. The intersection of these two groups, students who are both male and majoring in business, constitutes 10% of the total undergraduate population. Let $M$ be the event that a randomly selected undergraduate is male and let $B$ be the event that a randomly selected undergraduate is majoring in business.
    1. Compute $P(M|B)$ and $P(B|M)$. Interpret these results (include what the value is and what it represents in terms of the application).
    2. Are $M$ and $B$ independent? (justify your answer using the definition of independence from this section)
    Answer (click to Show/Hide)

    From the problem statement, we are given the following probabilities:

    $P(M)=0.48$

    $P(B)=0.18$

    $P(M\cap B)=0.10$

    a. Compute and interpret P(M|B) and P(B|M).

    First, we compute $P(M|B)$.
    This is the probability that a student is male, given that they are a business major.
    $$P(M|B)=\frac{P(M\cap B)}{P(B)}=\frac{0.10}{0.18}\approx 0.556$$
    Interpretation: About 55.6% of business majors at this university are male.

    Next, we compute $P(B|M)$.
    This is the probability that a student is a business major, given that they are male.
    $$P(B|M)=\frac{P(M\cap B)}{P(M)}=\frac{0.10}{0.48}\approx 0.208$$
    Interpretation: About 20.8% of male undergraduates at this university are majoring in business.

    Answer (a): $P(M|B)\approx 0.556$ and $P(B|M)\approx 0.208$.

    b. Are M and B independent?

    Two events M and B are independent if $P(M|B)=P(M)$. We can check if this condition is met using the values we have.

    From our calculation in part (a), $P(M|B)\approx 0.556$.

    We are given that $P(M)=0.48$.

    Since $0.556\ne 0.48$, the events are not independent.

    Answer (b): The events M and B are not independent because the probability that a student is male changes depending on whether or not they are a business major.

Attributions

• This page contains modified content from David Lippman, “Math In Society, 2nd Edition.” Licensed under CC BY-SA 4.0.
• This page contains modified content from “College Algebra 2017.” Lumen Learning. Licensed under CC BY 4.0.
• This page contains modified content from Introductory Statistics Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.
• This page contains content by Robert Foth, Math Faculty, Pima Community College, 2021. Licensed under CC BY 4.0.
• Portions of the exercise solutions in this answer key were generated with the assistance of Gemini, a large language model from Google.