2.1 Counting Methods
2.1: Counting Methods
Learning Objectives
Upon completion of this section, you should be able to
- Solve counting problems using the Addition Principle.
- Solve counting problems using the Multiplication Principle.
- Solve counting problems using permutations involving n distinct objects.
- Solve counting problems using combinations.
Addition Principle
Counting? You already know how to count or you wouldn’t be taking a college-level math class, right? Well yes, but what we’ll really be investigating here are ways of counting efficiently. When we get to the probability situations a bit later in this chapter we will need to count some very large numbers, like the number of possible winning lottery tickets. One way to do this would be to write down every possible set of numbers that might show up on a lottery ticket, but believe me: you don’t want to do this.
We encounter a wide variety of counting problems every day. There is a branch of mathematics devoted to the study of counting problems such as this one. Other applications of counting include secure passwords, horse racing outcomes, and college scheduling choices. We will examine this type of mathematics in this section
A company that sells customizable cases offers cases for tablets and smartphones. There are 3 supported tablet models and 5 supported smartphone models. The Addition Principle tells us that we can add the number of tablet options to the number of smartphone options to find the total number of options. By the Addition Principle, there are 8 total options.
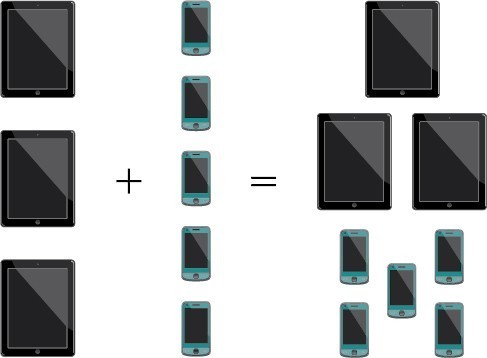
The Addition Principle
According to the Addition Principle, if one event can occur in m ways and a second event with no common outcomes can occur in n ways, then the first or second event can occur in ways.
Example 1
There are 2 vegetarian entrée options and 5 meat entrée options on a dinner menu. What is the total number of entrée options?
Solution
We can add the number of vegetarian options (2) to the number of meat options (5) to find the total number of entrée options. This gives us a total of 7 options.
Try it Now 1
A student is shopping for a new computer. She is deciding among 3 desktop computers and 4 laptop computers. What is the total number of computer options?
Answer (click to Show/Hide)
Add together the options for the desktop to the options for the laptop. The total number of options is 7.
Multiplication Principle
We will start with an example to illustrate the Multiplication Principle.
Example 2
Suppose at a particular restaurant you have three choices for an appetizer (soup, salad or breadsticks) and five choices for a main course (hamburger, sandwich, quiche, fajita or pasta). If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have?
Solution
Solution 1: One way to solve this problem would be to systematically list each possible meal:
| soup + hamburger | soup + sandwich | soup + quiche |
| soup + fajita | soup + pizza | salad + hamburger |
| salad + sandwich | salad + quiche | salad + fajita |
| salad + pizza | breadsticks + hamburger | breadsticks + sandwich |
| breadsticks + quiche | breadsticks + fajita | breadsticks + pizza |
Assuming that we did this systematically and that we neither missed any possibilities nor listed any possibility more than once, the answer would be 15. Thus you could go to the restaurant 15 nights in a row and have a different meal each night.
Solution 2: Another way to solve this problem would be to list all the possibilities in a table:
| hamburger | sandwich | quiche | fajita | pizza | |
| soup | soup+burger | ||||
| salad | salad+burger | ||||
| bread | etc. |
In each of the cells in the table we could list the corresponding meal: soup + hamburger in the upper left corner, salad + hamburger below it, etc. But if we didn’t really care what the possible meals are, only how many possible meals there are, we could just count the number of cells and arrive at an answer of 15, which matches our answer from the first solution. (It’s always good when you solve a problem two different ways and get the same answer!)
Solution 3: We already have two perfectly good solutions. Why do we need a third? The first method was not very systematic, and we might easily have made an omission. The second method was better, but suppose that in addition to the appetizer and the main course we further complicated the problem by adding desserts to the menu: we’ve used the rows of the table for the appetizers and the columns for the main courses—where will the desserts go? We would need a third dimension, and since drawing 3-D tables on a 2-D page or computer screen isn’t terribly easy, we need a better way in case we have three categories to choose form instead of just two.
So, back to the problem in the example. What else can we do? Let’s draw a tree diagram:
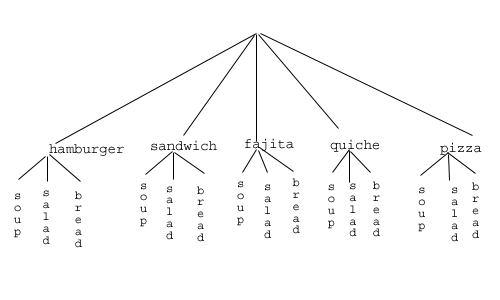
This is called a “tree” diagram because at each stage we branch out, like the branches on a tree. In this case, we first drew five branches (one for each main course) and then for each of those branches we drew three more branches (one for each appetizer). We count the number of branches at the final level and get (surprise, surprise!) 15.
If we wanted, we could instead draw three branches at the first stage for the three appetizers and then five branches (one for each main course) branching out of each of those three branches.
Video Solution (1 min 39 secs – CC) Another example starts after 1:39 mark on the video.
OK, so now we know how to count possibilities using tables and tree diagrams. These methods will continue to be useful in certain cases, but imagine a game where you have two decks of cards (with 52 cards in each deck) and you select one card from each deck. Would you really want to draw a table or tree diagram to determine the number of outcomes of this game?
Let’s go back to the previous example that involved selecting a meal from three appetizers and five main courses, and look at the second solution that used a table. Notice that one way to count the number of possible meals is simply to number each of the appropriate cells in the table, as we have done above. But another way to count the number of cells in the table would be multiply the number of rows (3) by the number of columns (5) to get 15. Notice that we could have arrived at the same result without making a table at all by simply multiplying the number of choices for the appetizer (3) by the number of choices for the main course (5). We generalize this technique as the Multiplication Principle, or sometimes called the Basic Counting Rule.
Multiplication Principle
If we are asked to choose one item from each of two separate categories where there are m items in the first category and n items in the second category, then the total number of available choices is .
This is sometimes called the Fundamental Counting Principle or Basic Counting Rule.
Example 3
There are 21 novels and 18 volumes of poetry on a reading list for a college English course. How many different ways can a student select one novel and one volume of poetry to read during the quarter?
Solution
There are 21 choices from the first category and 18 for the second, so there are possibilities.
Video Solution (1 min 8 secs – CC) Another example starts after 2:08 mark on the video.
The Multiplication Principle can be extended when there are more than two categories by applying it repeatedly, as we see in the next example.
Example 4
Suppose at a particular restaurant you have three choices for an appetizer (soup, salad or breadsticks), five choices for a main course (hamburger, sandwich, quiche, fajita or pasta) and two choices for dessert (pie or ice cream). If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have?
Solution
There are 3 choices for an appetizer, 5 for the main course and 2 for dessert, so there are possibilities.
Video Solution (2 mins 38 secs – CC) Another example starts after 2:38 mark on the video.
Example 5
A quiz consists of 3 true-or-false questions. In how many ways can a student answer the quiz?
Solution
There are 3 questions on the quiz. Each question has 2 possible answers (true or false), so the quiz may be answered in different ways.
Recall that another way to write is 23, which is much more compact.
Video Solution (41 secs – CC)
Try it Now 2
Suppose at a particular restaurant you have eight choices for an appetizer, eleven choices for a main course and five choices for dessert. If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have?
Hint 1 (click to Show/Hide)
Use the Fundamental Counting Principle here. We have three different categories for which options are available in each.
Answer (click to Show/Hide)
menu combinations
Permutations
The Multiplication Principle can be used to solve a variety of problem types. One type of problem involves placing objects in order. We arrange letters into words and digits into numbers, line up for photographs, decorate rooms, and more. An ordering of objects is called a permutation.
To solve permutation problems, it is often helpful to draw line segments for each option. That enables us to determine the number of each option so we can multiply. For instance, suppose we have four paintings, and we want to find the number of ways we can hang three of the paintings in order on the wall. We can draw three lines to represent the three places on the wall.

There are four options for the first place, so we write a 4 on the first line.

After the first place has been filled, there are three options for the second place so we write a 3 on the second line.
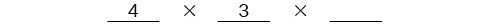
After the second place has been filled, there are two options for the third place so we write a 2 on the third line. Finally, we find the product.
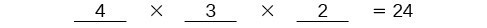
There are 24 possible permutations of the paintings.
Given n distinct options, determine how many permutations there are
- Determine how many options there are for the first situation.
- Determine how many options are left for the second situation.
- Continue until all of the spots are filled.
- Multiply the numbers together.
Example 6
At a swimming competition, nine swimmers compete in a race.
- How many ways can they place first, second, and third?
- How many ways can they place first, second, and third if a swimmer named Ariel wins first place? (Assume there is only one contestant named Ariel.)
- How many ways can all nine swimmers line up for a photo?
Solution
- Draw lines for each place.
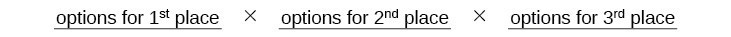
There are 9 options for first place. Once someone has won first place, there are 8 remaining options for second place. Once first and second place have been won, there are 7 remaining options for third place.
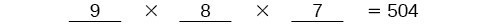
Multiply to find that there are 504 ways for the swimmers to place.
- Draw lines for describing each place.
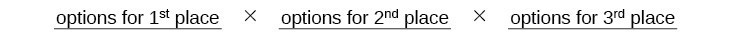
We know Ariel must win first place, so there is only 1 option for first place. There are 8 remaining options for second place, and then 7 remaining options for third place.
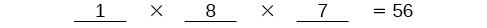
Multiply to find that there are 56 ways for the swimmers to place if Ariel wins first.
- Draw lines for describing each place in the photo.

There are 9 choices for the first spot, then 8 for the second, 7 for the third, 6 for the fourth, and so on until only 1 person remains for the last spot.
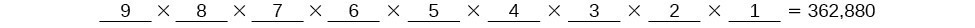
There are 362,880 possible permutations for the swimmers to line up.
In the above example, we needed to calculate . This calculation shows up often in mathematics, and is called a factorial, and is notated 9!.
Factorial
We define 0! = 1.
If you are wondring why 0!=1 we can think of 0! as representing the number of ways to arrange 0 items, and there is exactly 1 way to do this (do nothing).
Example 7
How many ways can five different door prizes be distributed among five people?
Solution
There are 5 choices of prize for the first person, 4 choices for the second, and so on. The number of ways the prizes can be distributed will be ways.
For some permutation problems, it is inconvenient to use the Multiplication Principle because there are so many numbers to multiply. Fortunately, we can solve these problems using a formula. Before we learn the formula, let’s look at two common notations for permutations. If we have a set of n objects and we want to choose r objects from the set in order, we write . Another way to write this is , a notation commonly seen on computers and calculators. To calculate , we begin by finding , the number of ways to line up all n objects. We then divide by to cancel out the items that we do not wish to line up.
Let’s see how this works with a simple example. Imagine a club of six people. They need to elect a president, a vice president, and a treasurer. Six people can be elected president, any one of the five remaining people can be elected vice president, and any of the remaining four people could be elected treasurer. The number of ways this may be done is . Using factorials, we get the same result.
There are 120 ways to select 3 officers in order from a club with 6 members. We refer to this as a permutation of 6 taken 3 at a time. The general formula is as follows.
Note that the formula stills works if we are choosing all n objects and placing them in order. In that case we would be dividing by or , which we said earlier is equal to 1. So the number of permutations of n objects taken n at a time is or just .
Permutations
A permutation of a set of elements is an ordered arrangement where each element is used once (or we can say without replacement). To find the number of permutations of r objects from n objects we use the given formula:
- Order of the elements being arranged matters (we would treat ABC and BAC as two distinct arrangements since they are in a different order)
- Without replacement: this means all items being arranged are considered distinct or unique (we would not have the same element repeated that we are picking from or any element used more than once)
- All positions in the arrangement are filled (can’t have an empty space in the arrangement)
In practicality, we usually use technology rather than factorials or repeated multiplication to compute permutations. Although with some calculations the technology may fail as the numbers can get extremely large.
Example 8
I have nine paintings and have room to display only four of them at a time on my wall. How many different ways could I do this?
Solution
Since we are choosing 4 paintings out of 9 without replacement where the order of selection is important there are permutations.
Video Solution (3 mins 6 secs – CC) Another example starts after 3:06 mark on the video.
Example 9
How many ways can a four-person executive committee (president, vice-president, secretary, treasurer) be selected from a 16-member board of directors of a non-profit organization?
Solution
We want to choose 4 people out of 16 without replacement and where the order of selection is important. So the answer is .
Video Solution (1 min 5 secs – CC)
Try it Now 3
How many 5 character passwords can be made using the letters A through Z
- if repeats are allowed
- if no repeats are allowed
Hint 1 (click to Show/Hide)
Think of this as having five categories for which we have options to fill in. In the first one part a we are told we are allowed to repeat the option from each category while in b we have a diminishing set of options (as you use one it can not be used again). Use the Fundamental Theorem of Counting / Principle to find the number in each situation.
Answer (click to Show/Hide)
There are 26 characters and five categories (slots) to fill.
- With repeats being allowed each category has 26 choices to fill in for the password. This gives us 265 = 11,881,376 ways to create the password.
- Here the first character for the password starts with 26 choices, but once we pick a character in the first slot we cannot use that character again (this is what it means by no repetition allowed). We can think of this as a permutation (order matters) in that we want to see how many ways we can pick five out of 26 with the order making a different password.
There are fewer passwords allowed without repetition and we end up with 7,893,600 possible passwords.
Combinations
So far, we have looked at problems asking us to put objects in order. There are many problems in which we want to select a few objects from a group of objects, but we do not care about the order. When we are selecting objects and the order does not matter, we are dealing with combinations. A selection of r objects from a set of n objects where the order does not matter can be written as . Just as with permutations, can also be written as . In this case, the general formula is as follows.
An earlier problem considered choosing 3 of 4 possible paintings to hang on a wall. We found that there were 24 ways to select 3 of the 4 paintings in order. But what if we did not care about the order? We would expect a smaller number because selecting paintings 1, 2, 3 would be the same as selecting paintings 2, 3, 1. To find the number of ways to select 3 of the 4 paintings, disregarding the order of the paintings, divide the number of permutations by the number of ways to order 3 paintings. There are ways to order 3 paintings. There are , or 4 ways to select 3 of the 4 paintings. This number makes sense because every time we are selecting 3 paintings, we are not selecting 1 painting. There are 4 paintings we could choose not to select, so there are 4 ways to select 3 of the 4 paintings.
Combinations
Given n distinct objects, the number of ways to select r objects where order does not matter from the set is
- Order of the elements being arranged does not matter (we would treat ABC and BAC as the same selection and gets only once as it is the same group of elements)
- Without replacement: this means all items being arranded are considered distinct or unique (we would not have the same element repeated that we are picking from or any element used more than once)
- All positions in the selection is filled (can’t have an empty space in the arrangement)
Example 10
A group of four students is to be chosen from a 35-member class to represent the class on the student council. How many ways can this be done?
Solution
Since we are choosing 4 people out of 35 without replacement where the order of selection is not important there are combinations.
Video Solution (4 mins 36 secs – CC)
Example 11
A fast food restaurant offers five side dish options. Your meal comes with two side dishes.
- How many ways can you select your side dishes?
- How many ways can you select 3 side dishes?
Solution
- We want to choose 2 side dishes from 5 options.
- We want to choose 3 side dishes from 5 options.
No. When we choose r objects from n objects, we are not choosing objects. Therefore, .
Try it Now 4
The United States Senate Appropriations Committee consists of 29 members; the Defense Subcommittee of the Appropriations Committee consists of 19 members. Disregarding party affiliation or any special seats on the Subcommittee, how many different 19-member subcommittees may be chosen from among the 29 Senators on the Appropriations Committee?
Hint 1 (click to Show/Hide)
As we are selecting does the order matter for which they appear? If Tom and Sally are both on the group is that different if we had said Sally and Tom are on the group? If the order doesn’t matter we are dealing with a combination question in this situation.
Answer (click to Show/Hide)
Order does not matter. possible subcommittees.
In the preceding Try it Now problem we assumed that the 19 members of the Defense Subcommittee were chosen without regard to party affiliation. In reality this would never happen: if Republicans are in the majority they would never let a majority of Democrats sit on (and thus control) any subcommittee. (The same of course would be true if the Democrats were in control.) So let’s consider the problem again, in a slightly more complicated form:
Example 12
The United States Senate Appropriations Committee consists of 29 members, 15 Republicans and 14 Democrats. The Defense Subcommittee consists of 19 members, 10 Republicans and 9 Democrats. How many different ways can the members of the Defense Subcommittee be chosen from among the 29 Senators on the Appropriations Committee?
Solution
In this case we need to choose 10 of the 15 Republicans and 9 of the 14 Democrats. There are 15C10 = 3003 ways to choose the 10 Republicans and 14C9 = 2002 ways to choose the 9 Democrats. But now what? How do we finish the problem?
Suppose we listed all of the possible 10-member Republican groups on 3003 slips of red paper and all of the possible 9-member Democratic groups on 2002 slips of blue paper. How many ways can we choose one red slip and one blue slip? This is a job for the Multiplication Principle! We are simply making one choice from the first category and one choice from the second category, just like in the restaurant menu problems from earlier.
There must be 3003 · 2002 = 6,012,006 possible ways of selecting the members of the Defense Subcommittee.
Video Solution (2 mins 18 secs – CC)
A coach selects three players from a team of 8 to represent the team at an award banquet is a combination problem as the three players selected do not have to be in any particular order. A problem where a coach select 3 players from a team of 8, but those three players will be wearing different uniforms would be a permutation problem as the same 3 players can be selected in a variety of ways by changing what uniform each wears (here the order was based on them having something different … we could have they were selected and arranged in order from #1 to #3.
Example 13
Permutation or Combination?
- How many ways can you select 5 free toys from a bucket of 200 toys?
- In a contest with 1000 players, in how many ways can the first three finishers come in?
Solution
- The toys being selected are not being ranked, so order does not matter. This is an example of a combination.
- Here the order in which a player finishes matters (first, second, third). Order matters, so this is an example of a permutation.
Exercises
- A person owns 4 pairs of pants, 8 shirts, 2 pairs of shoes, and 1 jacket. How many different outfits can they wear to school if they must wear one of each item?
Answer (click to Show/Hide)
This problem uses the Fundamental Counting Principle. To find the total number of possible outfits, we multiply the number of choices for each category of clothing together.
Step 1: Identify the number of choices for each item.
- Pants: 4 choices
- Shirts: 8 choices
- Shoes: 2 choices
- Jacket: 1 choice
Step 2: Multiply the number of choices.
We multiply the number of options for each item to find the total number of combinations.
Step 3: Calculate the final result.
Answer: The person can wear 64 different outfits.
- At a restaurant you can choose from 3 appetizers, 8 entrees, and 2 desserts. How many different three-course meals can you have if you must choose one of each?
Answer (click to Show/Hide)
This problem uses the Fundamental Counting Principle. To find the total number of possible meals, we multiply the number of choices for each course together.
Step 1: Identify the number of choices for each course.
- Appetizers: 3 choices
- Entrees: 8 choices
- Desserts: 2 choices
Step 2: Multiply the number of choices.
We multiply the number of options for each course to find the total number of combinations.
Step 3: Calculate the final result.
Answer: You can have 48 different three-course meals.
- How many three-letter “words” can be made from 4 letters “FGHI” if
- Repetition of letters is allowed
- Repetition of letters is not allowed
Answer (click to Show/Hide)
We will use the Fundamental Counting Principle to solve both parts of this problem.
a. Repetition of letters is allowed
When repetition is allowed, the number of choices for each position remains the same.
- For the first letter, there are 4 choices (F, G, H, or I).
- For the second letter, there are also 4 choices.
- For the third letter, there are again 4 choices.
To find the total number of possible words, we multiply the choices for each position:
b. Repetition of letters is not allowed
When repetition is not allowed, the number of choices decreases for each subsequent position.
- For the first letter, there are 4 choices.
- Once the first letter is chosen, there are only 3 choices remaining for the second letter.
- After the first two letters are chosen, there are 2 choices remaining for the third letter.
To find the total number of possible words, we multiply the choices for each position:
Answer:
a. If repetition is allowed, 64 three-letter words can be made.
b. If repetition is not allowed, 24 three-letter words can be made. - How many four-letter “words” can be made from 6 letters “AEBWDP” if
- Repetition of letters is allowed
- Repetition of letters is not allowed
Answer (click to Show/Hide)
We will use the Fundamental Counting Principle to solve both parts of this problem.
a. Repetition of letters is allowed
When repetition is allowed, the number of choices for each position remains the same.
- For the first letter, there are 6 choices (A, E, B, W, D, or P).
- For the second letter, there are also 6 choices.
- For the third letter, there are again 6 choices.
- For the fourth letter, there are 6 choices.
To find the total number of possible words, we multiply the choices for each position:
b. Repetition of letters is not allowed
When repetition is not allowed, the number of choices decreases for each subsequent position.
- For the first letter, there are 6 choices.
- Once the first letter is chosen, there are only 5 choices remaining for the second letter.
- After the first two letters are chosen, there are 4 choices remaining for the third letter.
- After the first three letters are chosen, there are 3 choices remaining for the fourth letter.
To find the total number of possible words, we multiply the choices for each position:
Answer:
a. If repetition is allowed, 1296 four-letter words can be made.
b. If repetition is not allowed, 360 four-letter words can be made. - All of the license plates in a particular state feature three letters followed by three digits (e.g. ABC 123). How many different license plate numbers are available to the state’s Department of Motor Vehicles?
Answer (click to Show/Hide)
This problem uses the Fundamental Counting Principle. We need to determine the number of choices for each of the six positions on the license plate and then multiply them together. Repetition is allowed for both letters and digits.Step 1: Identify the number of choices for each position.
There are 26 letters in the alphabet (A-Z) and 10 digits (0-9).- Position 1 (Letter): 26 choices
- Position 2 (Letter): 26 choices
- Position 3 (Letter): 26 choices
- Position 4 (Digit): 10 choices
- Position 5 (Digit): 10 choices
- Position 6 (Digit): 10 choices
Step 2: Set up the multiplication.
We multiply the number of choices for each of the six positions to find the total number of possible license plates.
Step 3: Calculate the final result.
This can be simplified using exponents and then calculated.
Answer: There are 17,576,000 different license plate numbers available.
- A computer password must be eight characters long. How many passwords are possible if only the 26 letters of the alphabet are allowed?
Answer (click to Show/Hide)
This problem uses the Fundamental Counting Principle. Since repetition of letters is allowed in a password, the number of choices for each of the eight positions remains the same.
Step 1: Identify the number of choices for each position.
There are 26 letters in the alphabet.- Position 1: 26 choices
- Position 2: 26 choices
- Position 3: 26 choices
- Position 4: 26 choices
- Position 5: 26 choices
- Position 6: 26 choices
- Position 7: 26 choices
- Position 8: 26 choices
Step 2: Set up the multiplication.
To find the total number of possible passwords, we multiply the number of choices for each of the eight positions.
Step 3: Calculate the final result.
This can be simplified using exponents.
Answer: There are 208,827,064,576 possible passwords.
- A pianist plans to play 4 pieces at a recital. In how many ways can she arrange these pieces in the program?
Answer (click to Show/Hide)
This is a permutation problem because the order in which the pieces are played matters. We are arranging 4 distinct items.
Method 1: Fundamental Counting Principle
Step 1: Identify the number of choices for each position in the program.
- For the first piece, the pianist has 4 choices.
- After choosing the first piece, there are 3 choices remaining for the second piece.
- After the first two are chosen, there are 2 choices for the third piece.
- Finally, there is only 1 choice left for the last piece.
Step 2: Multiply the choices.
We multiply the number of choices for each position to find the total number of arrangements. This calculation is also known as a factorial, written as 4!.
Method 2: Permutation Formula
The number of permutations of n items taken r at a time is given by the formula:
In this problem, we are arranging all 4 pieces, so n = 4 and r = 4.
(Note: By definition, 0! = 1)Answer: There are 24 different ways the pianist can arrange the pieces in the program.
- In how many ways can first, second, and third prizes be awarded in a contest with 210 contestants?
Answer (click to Show/Hide)
This is a permutation problem because the order of selection matters (first, second, and third prizes are distinct). We are selecting and arranging 3 people out of 210.
Method 1: Fundamental Counting Principle
Step 1: Identify the number of choices for each prize.
- For first prize, there are 210 contestants to choose from.
- After the first prize winner is chosen, there are 209 contestants left for second prize.
- After the second prize winner is chosen, there are 208 contestants left for third prize.
Step 2: Multiply the choices.
We multiply the number of choices for each prize to find the total number of ways the prizes can be awarded.
Method 2: Permutation Formula
The number of permutations of n items taken r at a time is given by the formula:
In this problem, we are choosing 3 winners from 210 contestants, so n = 210 and r = 3.Answer: There are 9,129,120 ways to award the prizes.
- Seven Olympic sprinters are eligible to compete in the 4 x 100 m relay race for the USA Olympic team. How many four-person relay teams can be selected from among the seven athletes?
Answer (click to Show/Hide)
This is a permutation problem because the order in which the athletes run the legs of the relay matters. A team with athlete A running the first leg and B running the second is different from a team with B running first and A running second. We are arranging 4 athletes out of a group of 7.
Method 1: Fundamental Counting Principle
Step 1: Identify the number of choices for each leg of the relay.
- For the first leg, there are 7 athletes to choose from.
- After the first runner is chosen, there are 6 athletes left for the second leg.
- After the second runner is chosen, there are 5 athletes left for the third leg.
- Finally, there are 4 athletes left for the fourth leg (the anchor).
Step 2: Multiply the choices.
We multiply the number of choices for each position to find the total number of possible relay teams.
Method 2: Permutation Formula
The number of permutations of n items taken r at a time is given by the formula:
In this problem, we are arranging 4 runners from a group of 7, so n = 7 and r = 4.
Answer: There are 840 different four-person relay teams that can be selected.
- A computer user has downloaded 25 songs using an online file-sharing program and wants to create a CD-R with ten songs to use in his portable CD player. If the order that the songs are placed on the CD-R is important to him, how many different CD-Rs could he make from the 25 songs available to him?
Answer (click to Show/Hide)
This problem involves selecting and arranging a subset of items from a larger group where the order of selection is important. This is a permutation. We need to find the number of permutations of 25 songs taken 10 at a time.
Method: Permutation Formula
The number of permutations of n items taken r at a time is given by the formula:
In this problem, we are arranging 10 songs from a group of 25, so n = 25 and r = 10.
Answer: There are 11,861,676,288,000 different CD-Rs that could be made.
-
In western music, an octave is divided into 12 pitches (notes). For the film Close Encounters of the Third Kind, director Steven Spielberg asked composer John Williams to write a five-note theme, which aliens would use to communicate with people on Earth. If we stay in the same octave and disregard rhythm changes, how many five-note themes are possible if no pitch (note) is repeated?
Answer (click to Show/Hide)
This problem asks for the number of ways to arrange 5 notes from a selection of 12, where the order of the notes matters and notes cannot be repeated. This is a permutation.
Method 1: Fundamental Counting Principle
- For the first note, there are 12 choices.
- Since no note is repeated, there are 11 choices remaining for the second note.
- For the third note, there are 10 choices remaining.
- For the fourth note, there are 9 choices remaining.
- For the fifth note, there are 8 choices remaining.
To find the total number of themes, we multiply the choices together:
Method 2: Permutation Formula
The number of permutations of n items taken r at a time is given by the formula:
In this problem, we are arranging 5 notes from a group of 12, so n = 12 and r = 5.
Answer: There are 95,040 possible five-note themes.
- In the early twentieth century, proponents of the Second Viennese School of musical composition (including Arnold Schönberg, Anton Webern and Alban Berg) devised the twelve-tone technique, which utilized a tone row consisting of all 12 pitches from the chromatic scale in any order, but with no pitches repeated in the row. Disregarding rhythm and octave changes, how many tone rows are possible?
Answer (click to Show/Hide)
This problem asks for the number of ways to arrange all 12 pitches from the chromatic scale, where order is important and no pitch is repeated. This is a permutation of 12 items taken 12 at a time, which is equivalent to a factorial.
Method 1: Fundamental Counting Principle
- For the first note in the row, there are 12 choices.
- For the second note, there are 11 choices remaining.
- This continues until the last note, for which there is only 1 choice remaining.
To find the total number of tone rows, we multiply the choices for each position:
Method 2: Permutation Formula
The number of permutations of n items taken r at a time is given by the formula:
In this problem, we are arranging 12 pitches from a group of 12, so n = 12 and r = 12.
(Remember that 0! is defined as 1.)Answer: There are 479,001,600 possible tone rows.
- In how many ways can 4 pizza toppings be chosen from 12 available toppings?
Answer (click to Show/Hide)
This problem involves selecting a group of items where the order of selection does not matter. For example, choosing pepperoni, mushrooms, olives, and onions is the same as choosing olives, pepperoni, onions, and mushrooms. This is a combination problem.
Method: Combination Formula
The number of combinations of n items taken r at a time is given by the formula:
In this problem, we are choosing 4 toppings from a group of 12, so n = 12 and r = 4.
Answer: There are 495 ways to choose 4 pizza toppings from 12.
- At a baby shower 17 guests are in attendance and 5 of them are randomly selected to receive a door prize. If all 5 prizes are identical, in how many ways can the prizes be awarded?
Answer (click to Show/Hide)
This problem involves selecting a group of people where the order of selection does not matter because all the prizes are identical. This is a combination problem.
Method: Combination Formula
The number of combinations of n items taken r at a time is given by the formula:
In this problem, we are choosing 5 guests from a group of 17, so n = 17 and r = 5.
Answer: There are 6,188 ways the prizes can be awarded.
- In the 6/50 lottery game, a player picks six numbers from 1 to 50. How many different choices does the player have if order doesn’t matter?
Answer (click to Show/Hide)
This problem involves selecting a group of numbers where the order of selection does not matter. This is a combination problem.
Method: Combination Formula
The number of combinations of n items taken r at a time is given by the formula:
In this problem, we are choosing 6 numbers from a group of 50, so n = 50 and r = 6.
Answer: The player has 15,890,700 different choices.
- In a lottery daily game, a player picks three numbers from 0 to 9. How many different choices does the player have if order doesn’t matter?
Answer (click to Show/Hide)
This problem involves selecting a group of numbers where the order of selection does not matter. This is a combination problem. The numbers to choose from are {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, which is a set of 10 numbers.
Method: Combination Formula
The number of combinations of n items taken r at a time is given by the formula:
In this problem, we are choosing 3 numbers from a group of 10, so n = 10 and r = 3.
Answer: The player has 120 different choices.
- A jury pool consists of 27 people. How many different ways can 11 people be chosen to serve on a jury and one additional person be chosen to serve as the jury foreman?
Answer (click to Show/Hide)
This is a two-step counting problem. First, we select the group of jurors, and then we select the foreman from the remaining people.
Step 1: Choose the jurors.
The order in which the 11 jurors are chosen does not matter, so this is a combination. We need to find the number of ways to choose 11 people from a pool of 27.
There are 13,037,895 ways to choose the 11 jurors.Step 2: Choose the jury foreman.
After the 11 jurors are chosen, there are people remaining in the pool. One of these people must be chosen as the foreman.
There are 16 choices for the foreman.Step 3: Find the total number of ways.
Using the Fundamental Counting Principle, we multiply the number of ways to complete each step.
Answer: There are 208,606,320 different ways to choose the jury and the foreman.
An alternative approach to this is look at how many ways there are to select 12 jurors out of the 27 and then multiply by the number of ways to select 1 of those 12 to be the forman. Both yield the same results (try this to see if you get the same answer).
- The United States Senate Committee on Commerce, Science, and Transportation consists of 23 members, 12 Republicans and 11 Democrats. The Surface Transportation and Merchant Marine Subcommittee consists of 8 Republicans and 7 Democrats. How many ways can members of the Subcommittee be chosen from the Committee?
Answer (click to Show/Hide)
This problem requires us to choose two separate groups (Republicans and Democrats) and then combine the results. Since the order of selection for a committee does not matter, this is a combination problem.
Step 1: Choose the Republican members.
We need to choose 8 Republicans from the 12 available on the main committee.
There are 495 ways to choose the Republican members.Step 2: Choose the Democratic members.
We need to choose 7 Democrats from the 11 available on the main committee.
There are 330 ways to choose the Democratic members.Step 3: Find the total number of ways.
Using the Fundamental Counting Principle, we multiply the number of ways to form each group.
Answer: There are 163,350 ways to choose the members of the Subcommittee.
Attributions
- This page contains modified content from David Lippman, “Math In Society, 2nd Edition.” Licensed under CC BY-SA 4.0.
- This page contains modified content from “College Algebra 2017.” Lumen Learning. Licensed under CC BY 4.0.
- This page contains content by Robert Foth, Math Faculty, Pima Community College, 2021. Licensed under CC BY 4.0.
- Portions of the exercise solutions in this answer key were generated with the assistance of Gemini, a large language model from Google.

