1.3 Proportional Reasoning

Robert Foth

1.3 Proportional Reasoning

1.3: Proportional Reasoning

Learning Objectives

Upon completion of this section, you should be able to

Solve proportions.
Solve application problems involving proportions.
Identify when a proportion equation should not be used.
Solve application problems involving similar triangles.

Proportions

If you wanted to power the city of Seattle using wind power, how many windmills would you need to install? A question like this can be answered using proportions if you know how much power Seattle uses and how much power you can create with one windmill. In this section we are going to look at how we can use proportions to solve some application problems.

When you apply for a mortgage, the loan officer will compare your total debt to your total income to decide if you qualify for the loan. This comparison is called the debt-to-income ratio. A ratio compares two quantities that are measured with the same unit. If we compare a and b, the ratio is written as $a to b, \frac{a}{b}, or a : b$

Ratio

A ratio compares two numbers or two quantities that are measured with the same (or similar) units. The ratio of a to b is written as $a to b, \frac{a}{b}, or a : b$

When a ratio is written in fraction form, the fraction should be simplified in most cases. If it is an improper fraction, we do not change it to a mixed number for the calculations, but we may change it to a mixed number if it better helps explain the meaning of the answer to the reader. Whether we simplify or write answers as a mixed number is really more about how it will be used. For instance, if a recipe calls for 4 cups of flour and 1 cup of sugar, the ratio of flour to sugar can be written as the fraction $\frac{4}{1}$ . In this case, we would not want to simplify the fraction to 4, as the intent is to communicate the specific ratio of 4 parts flour to 1 part sugar. The improper fraction form better represents the original quantities.

Frequently we want to compare two different types of measurements, such as miles to gallons. A rate is a special type of ratio that is a comparison of two quantities with different units to give us information, such as miles per gallon, words per minute, or dollars per ounce.

Rate

A rate compares two quantities of different units. A rate is usually written as a fraction.

When writing a fraction as a rate, we put the first given amount with its units in the numerator and the second amount with its units in the denominator. When rates are simplified, the units remain in the numerator and denominator. For example if Bob drove his car 525 miles in 9 hours we can express this information as a rate $\frac{525 miles}{9 hours}$ or as $\frac{175 miles}{3 hours}$ when simplified.

When two ratios or rates are equal, the equation relating them is called a proportion. Remember a ratio compares two quantities that have the same units where a rate compares 2 quantities with different units

Proportion

A proportion is an equation showing the equivalence of two rates or ratios. A proportion equation has the form

$\frac{a}{b} = \frac{c}{d}$ , where

$b \neq 0 and d \neq 0$ .

The proportion is read “a is to b, as c is to d“.

The equation $\frac{1}{2} = \frac{4}{8}$ is a proportion because the two fractions are equal. The proportion $\frac{1}{2} = \frac{4}{8}$ is read “1 is to 2 as 4 is to 8”.

If we compare quantities with units, we have to be sure we are comparing them in the right order. For example,
in the proportion $\frac{20 student}{1 teacher} = \frac{60 student}{3 teacher}$ we compare the number of students to the number of teachers. We put students in the numerators and teachers in the denominators.

Solve Proportions

If $\frac{a}{b}$ and $\frac{c}{d}$ are two ratios such that $\frac{a}{b} = \frac{c}{d}$ then the fractions are said to be proportional. Also, two fractions $\frac{a}{b}$ and $\frac{c}{d}$ are proportional $(\frac{a}{b} = \frac{c}{d})$ if and only if $a \cdot d = b \cdot c$ .

Solving a Proportion Equation

Variable in Numerator:

Multiply both sides of the equation by the denominator under the variable. Simplify the results and isolate
the variable further if needed.

$\begin{array}{l} \frac{x}{b} = \frac{c}{d} \\ b \cdot (\frac{x}{b}) = b \cdot (\frac{c}{d}) \\ x = \frac{b \cdot c}{d} \end{array}$

Variable in Denominator:

Cross Multiply both sides of the equation. Isolate the variable and simplify the results.

$\begin{array}{l} \frac{a}{x} = \frac{c}{d} \\ a \cdot d = c \cdot x \\ \frac{a \cdot d}{c} = x \end{array}$

Example 1

Solve the proportion $\frac{5}{3} = \frac{x}{6}$ for the unknown value x.

Solution

This proportion is asking us to find a fraction with denominator 6 that is equivalent to the fraction $\frac{5}{3}$ . We can solve this by multiplying both sides of the equation by 6 (our denominator under the variable) and simplifying the result.

$\begin{array}{l} \frac{5}{3} = \frac{x}{6} \\ 6 \cdot \frac{5}{3} = x \\ (3 \cdot 2) \frac{5}{3} = x \\ 10 = x \end{array}$

Example 2

Solve the proportion $\frac{144}{a} = \frac{9}{4}$ for the unknown value a.

Solution

In this case our variable is in the denominator so we start by cross multiplying. $144 \cdot 4 = 9 \cdot a$ Now we just isolate the variable by dividing through by 9 on both sides and simplifying the result.

$\begin{array}{l} \frac{144 \cdot 4}{9} = a \\ \frac{(16 \cdot 9) 4}{9} = a \\ 64 = a \end{array}$

Try it Now 1

Solve the following:

$\frac{n}{4} = \frac{11}{12}$
$\frac{84}{98} = \frac{- 6}{x}$

Answer (click to Show/Hide)

Variable is in the numerator, so start by multiplying both sides of the equation by 4 and simplify the results
$\begin{array}{l} \frac{n}{4} = \frac{11}{12} \\ 4 \cdot (\frac{n}{4}) = 4 \cdot (\frac{11}{12}) \\ n = \frac{4 \cdot 11}{4 \cdot 3} \\ n = \frac{4 \cdot 11}{4 \cdot 3} \\ n = \frac{11}{3} \end{array}$
Variable is in the denominator, so start with cross multiplying
$\begin{array}{l} \frac{84}{98} = \frac{- 6}{x} \\ x \cdot 84 = - 6 \cdot 98 \\ x = \frac{- 6 \cdot 98}{84} \\ x = \frac{- 2 \cdot 3 \cdot 2 \cdot 7 \cdot 7}{3 \cdot 2 \cdot 2 \cdot 7} \\ x = \frac{- 2 \cdot 3 \cdot 2 \cdot 7 \cdot 7}{3 \cdot 2 \cdot 2 \cdot 7} \\ x = - 7 \end{array}$

Solve Application Problems Involving Proportions

Using proportions to solve problems is a very useful method. It is usually used when you know three parts of the proportion, and one part is unknown. Proportions are often solved by setting up like ratios. When we set up the proportion, we must make sure the units are correct—the units in the numerators match and the units in the denominators match.

To determine when you can use a proportional equation

Constant Ratio

This means that as one quantity changes, the other changes in such a way that their ratio remains the same.
For example, if you’re driving at a constant speed of 60 mph, the ratio of distance to time will always be 60 miles to 1 hour.
You can check this by dividing one quantity by the other at different points – if it’s always the same, it’s likely proportional.

Linear relationship

When graphed on a coordinate plane, proportional relationships form a straight line.
This line always passes through the origin (0,0), meaning when one quantity is zero, the other is also zero.

Zero pair

In a proportional relationship, if one quantity is zero, the other must also be zero.
This is why the graph passes through the origin.
For instance, if you buy zero apples, you pay zero dollars.

Scaling property

If you multiply or divide one quantity by a number, the other quantity is multiplied or divided by the same number to maintain the proportion.
For example, if you double the number of apples purchased, you double the price paid.

Common examples of proportional relationships:

Distance and time at constant speed
Cost and quantity of items at a fixed price
Recipe ingredients when scaling up or down
Scale models and actual objects
Currency exchange rates (in ideal conditions)
Voltage and current in a resistor (Ohm’s Law)

Examples of non-proportional relationships:

Age and height of a person
Temperature in Celsius and Fahrenheit
Distance and time when not at a constant speed
Income tax paid (progressive like AZ income taxes)
Area of a square and its side length (quadratic relationship)
Population growth over time (often exponential)

Example 3

A type 1 diabetic needs to keep track of the amount of carbs in a given meal to determine the correct insulin dosage to give themselves (along with other factors like their current blood sugar reading). A small Lemon Eegee is 16 oz and is listed to have 47 carbs. How many carbs would be in a Bigee that is 44 oz?

Solution

In this situation we do expect the amount of carbs and the size of the drink to have a proportional relationship. We can set up a proportion by setting equal two ratios that would be equivalent (ratio of carbs per serving size). We are given there is 47 carbs per 16 oz of Eegee and we want to find an unknown number of carbs, call it c, in a 44 oz size Eegee. This gives us:

$\frac{47 carbs}{16 oz} = \frac{c carbs}{44 oz}$

With the variable in the numerator we multiply both sides by 44 and simplify (solve):

$\begin{array}{l} 44 \cdot \frac{47}{16} = c \\ 129.25 = c \end{array}$

A 44 oz Eegee would contain approximately 129 carbs (when rounded to nearest integer).

Example 4

One brand of microwave popcorn has 120 calories per serving. A whole bag of this popcorn has 3.5 servings. How many calories are in a whole bag of this microwave popcorn?

Solution

We can set up a proportion by setting equal two ratios that would be equivalent (ratio of calories per serving). Now we are given there are 120 calories per one serving and we want to find an unknown number of calories, call it x, in a whole bag. The whole bag itself has 3.5 servings. This gives us:

$\frac{120 calories}{1 serving} = \frac{x calories}{3.5 serving}$

The variable is in the numerator, so we multiply both sides by 3.5 and then solve.

$\begin{array}{l} \frac{120}{1} = \frac{x}{3.5} \\ 3.5 (120) = x \\ 420 = x \end{array}$

This tells us there is 420 calories in the whole bag of popcorn.

Example 5

A map scale indicates that ½ inch on the map corresponds with 3 real miles. How many miles apart are two cities that are $2 \frac{1}{4}$ inches apart on the map?

Solution

We can set up a proportion by setting equal two $\frac{map inches}{real miles}$ rates, and introducing a variable, x, to represent the unknown quantity – the mile distance between the cities.

We can set up a proportion where:
$\frac{1 / 2 inch}{3 miles} = \frac{2 \frac{1}{4} inches}{x miles}$

Before we start solving we need to rewrite the mixed number $2 \frac{1}{4}$ inches into an improper fraction as we don’t want to treat this like multiplication. This reprsents two and a quarter inches, so we can think of it as $2 + \frac{1}{4}$ inches or $2 + \frac{1}{4} = \frac{8}{4} + \frac{1}{4} = \frac{9}{4}$ inches.

Now our equation looks like

$\frac{\frac{1}{2}}{3} = \frac{\frac{9}{4}}{x}$

Next we can cross multiply
$\frac{1}{2} \cdot x = 3 \cdot \frac{9}{4}$

Solve for x

$\begin{array}{l} \frac{1}{2} \cdot x = 3 \cdot \frac{9}{4} \\ \frac{1}{2} \cdot x = \frac{27}{4} \end{array}$

To solve for x, multiply both sides by 2

$\begin{array}{l} x = 2 \cdot \frac{27}{4} \\ x = \frac{27}{2} \end{array}$

We can now rewrite as a mixed number to be more reader friendly.

$x = 13 \frac{1}{2} miles or we can say 13 .5 miles$

Video Solution(3 min 8 secs – CC)

Try it Now 2

When pediatricians prescribe acetaminophen (a type of pain reliever) to children, they prescribe 5 milliliters (ml) of acetaminophen for every 25 pounds of the child’s weight. If Zoe weighs 80 pounds, how many milliliters of acetaminophen will her doctor prescribe?

Hint 1 (click to Show/Hide)

The proportion of medicine to weight makes sense to be equal to each other in many cases (not always, but in this case it would be safe to assume so).

Hint 2 (click to Show/Hide)

The proportion equation can be set up in two ways. It doesn’t matter which one you choose, but at times one form is easier to solve over the other (typically when you put the variable in the numerator). Let x be the amount of acetaminophen (in ml).

$\begin{array}{l} \frac{5 ml}{25 pounds} = \frac{x ml}{80 pounds} \\ or \\ \frac{25 pounds}{5 ml} = \frac{80 pounds}{x ml} \end{array}$

Answer (click to Show/Hide)

Using the proportional equation where x (the amount of acetaminophen) is in the numerator we can solve.

$\begin{array}{l} \frac{5 ml}{25 pounds} = \frac{x ml}{80 pounds} \\ \frac{5}{25} = \frac{x}{80} \\ 80 \cdot (\frac{5}{25}) = x \\ (16 \cdot 5) (\frac{5}{5 \cdot 5}) = x \\ 16 = x \end{array}$

The pediatrician would prescribe 16 ml of acetaminophen to Zoe.

Errors Using Proportional Equations

We can’t always jump to a proportional equation for every problem. In many cases the relationship between two values may not be equal to each other. For instance a car has a certain points for which the fuel efficiency is at its best and then beyond those values the vehicle will use the fuel at a faster rate. So we can’t set up a proportional equation to find the amount gas used when driving at 50 mph for one hour compared to driving 90 mph for one hour. However in some situations we may be able to change the variables that are related around to solve using a proportional equation (like in the next example).

Not all relationships between variables can be represented by proportional equations. In many real-world scenarios, the relationship between two values is not constant or linear. Understanding when a relationship is not proportional is crucial for accurate problem-solving.

Examples of Non-Proportional Relationships

`Example 1: Car Fuel Efficiency
A car’s fuel efficiency is not proportional to its speed. At moderate speeds, a car may achieve optimal fuel efficiency. However, as speed increases beyond this optimal range, fuel consumption increases at a faster rate. For instance:

Driving at 50 mph for one hour might consume 2 gallons of fuel
Driving at 90 mph for one hour might consume 4.5 gallons of fuel

This relationship cannot be represented by a simple proportional equation.

Example 2: Plant Growth
The growth of a plant is not proportional to the amount of water it receives. While water is essential for plant growth, the relationship is more complex:

Too little water will stunt growth
An optimal amount of water will promote healthy growth
Too much water can be harmful and even kill the plant

This non-linear relationship demonstrates why a proportional equation would not accurately model plant growth in relation to water intake.

Example 6

Suppose you’re tiling the floor of a 10 ft by 10 ft room, and find that 100 tiles will be needed. How many tiles will be needed to tile the floor of a 20 ft by 20 ft room?

Solution

This problem illustrates an important concept: the relationship between linear dimensions and area. Let’s break it down step by step:

It might be tempting to set up a proportional equation based on the room’s width, but this would be incorrect. The number of tiles needed corresponds to the room’s area, not its width.

Calculate the areas

10 ft × 10 ft room: Area = 100 sq ft
20 ft × 20 ft room: Area = 400 sq ft

Notice that while the width doubled, the area quadrupled.

We can now set up a proportion based on the areas and the number of tiles:

In this case it may be tempting to set up a proportional equation based on the number of tiles and the width in the room. This will not however work as those proportions will not be equal as the width changes. The width in the room has doubled, but the area has quadrupled. Since the number of tiles needed corresponds with the area of the floor, not the width, 400 tiles will be needed. We could find this using a proportion based on the areas of the rooms:

$\frac{100 tiles}{100 {ft}^{2}} = \frac{n tiles}{400 {ft}^{2}}$

Cross-multiplying and solving for n

$\begin{array}{rcl} 100 \cdot 400 & = & 100 \cdot n \\ \frac{100 \cdot 400}{100} & = & n \\ 400 & = & n \end{array}$

400 tiles will be needed for the 20 ft by 20 ft room.

Video Solution (2 mins 11 secs – CC) Another example starts after the 2:11 mark of the video.

Other quantities just don’t scale proportionally at all.

Example 7

Suppose a small company spends $1000 on an advertising campaign, and gains 100 new customers from it. How many new customers should they expect if they spend $10,000?

Solution

While it is tempting to say that they will gain 1000 new customers, it is likely that additional advertising will be less effective than the initial advertising. For example, if the company is a hot tub store, there are likely only a fixed number of people interested in buying a hot tub, so there might not even be 1000 people in the town who would be potential customers.

Video Solution(1 min 6 secs – CC)

Solve Application Problems Involving Similar Triangles

Geometric shapes, as well as area and volumes, can often be important in problem solving. In some cases we can solve a problem by working with two dimensional shapes while in others we need to think three dimensional. It is important on many of these to try to draw a diagram to determine which types of formulas you will want to use.

One strategy for working with some problems is to use the idea of similar triangles. If two triangles have the same angles inside we say they are similar and this means that each side is proportional to each other. That means we can set up a relation between the ratio of two sides between the two triangles as long as those sides come from the same sides corresponding to the same angles.

Properties of Similar Triangles

If two triangles are similar, then their corresponding angle measures are equal and their corresponding side lengths are in the same ratio.

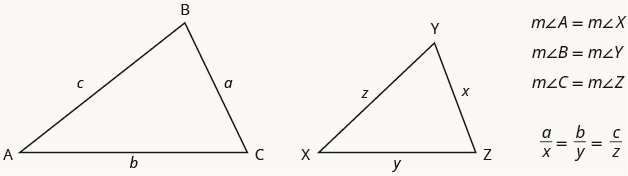
Two triangles are shown. They appear to be the same shape, but the triangle on the right is smaller. The vertices of the triangle on the left are labeled A, B, and C. The side across from A is labeled a, the side across from B is labeled b, and the side across from C is labeled c. The vertices of the triangle on the right are labeled X, Y, and Z. The side across from X is labeled s, the side across from Y is labeled y, and the side across from Z is labeled z. Beside the triangles, it says that the measure of angle A equals the measure of angle X, the measure of angle B equals the measure of angle Y, and the measure of angle C equals the measure of angle Z. Below this is the proportion a over x equals b over y equals c over z

Just a note on notation. When we write $m ∠ A .$ this means the measure of angle A or the value of angle A.

Example 8

$Δ A B C$ and $Δ X Y Z$ are similar triangles. We also know that $m ∠ A$ and $m ∠ X$ are equal to each other. The lengths of two sides of each triangle are shown. Find the lengths of the third side of each triangle.

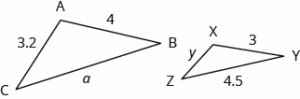
Solution

The triangles are similar, so the corresponding sides are in the same ratio. So

$\frac{A B}{X Y} = \frac{B C}{Y Z} = \frac{A C}{X Z}$

Since the side $A B = 4$ corresponds to the side $X Y = 3$ , we will use the ratio $\frac{AB}{XY} = \frac{4}{3}$ to find the other sides.

To find a:

$\begin{array}{rcl} \frac{A B}{X Y} & = & \frac{B C}{Y Z} \\ \frac{4}{3} & = & \frac{a}{4.5} \end{array}$

Next solve the equation for a

$\begin{array}{rcl} 4.5 \cdot \frac{4}{3} & = & a \\ 6 & = & a \end{array}$

To find y:

$\begin{array}{rcl} \frac{A B}{X Y} & = & \frac{A C}{X Z} \\ \frac{4}{3} & = & \frac{3.2}{y} \end{array}$

Next solve the equation for a

$\begin{array}{rcl} 4 \cdot y & = & 3 \cdot 3.2 \\ y & = & \frac{9.6}{4} \\ y & = & 2.4 \end{array}$

The third side of $Δ A B C$ is 6 and the third side of $Δ X Y Z$ is 2.4.

In the first example you will see a classic problem of measuring the height of an object by setting up a similar triangles.

Example 9

You are curious how tall a tree is, but don’t have any way to climb it. Suppose the tree is casting a shadow that is 15 ft long. A person standing by the tree is 6 ft tall and casts a shadow that is 1.5 ft long. How tall is that tree?

Solution

There are several approaches we could take. We’ll use one based on triangles, which requires that it’s a sunny day. Since the triangle formed by the tree and its shadow has the same angles as the triangle formed by me and my shadow, these triangles are called similar triangles and their sides will scale proportionally. In other words, the ratio of height to width will be the same in both triangles. Using this, we can find the height of the tree, which we’ll denote by h:

$\frac{6 ft tall}{1.5 ft shadow} = \frac{h ft tall}{15 ft shadow}$ Multiplying both sides by 15, we get h = 60. The tree is about 60 ft tall.

Video Solution(2 mins 19 secs – CC)

Try it Now 3

A person who is 6 feet tall is standing 100 feet away from the base of a tree. The tree casts a shadow 107.5-foot shadow. The person’s shadow is 7.5 feet long. How tall is the tree?

An illustration of a palm tree and a stick figure person shows a right triangle. The vertical leg shows a tree. The hypotenuse is unknown. The horizontal leg measures 107.5 feet. A boy who is 6 feet tall is standing 100 feet away from the base of the tree. The boy casts a shadow of 7.5 feet.

Hint 1 (click to Show/Hide)

The tree and the shadow of the tree forms a similar triangle with the person and the persons shadow. This means the ratio of the heights of the tree and person is equivalent to the ratio of the length of shadow of the tree to the length of shadow of the person.

Answer (click to Show/Hide)

With the tree and person forming a similar triangle with their shadows we can set up a proportional equation where the unknown height of the tree is denoted with x.

$\frac{x trees height in ft}{6 persons height in ft} = \frac{107.5 shadow of trees length in ft}{7.5 shadow of persons length in ft}$

Multiply both sides by 6:

$x = 6 \cdot \frac{107.5}{7.5}$

$x = 86$

The height of the tree is 86ft.

Exercises

Solve: $\frac{2}{5} = \frac{6}{x}$

Answer (click to Show/Hide)

x = 15
Solve: $\frac{y}{96} = \frac{13}{12}$

Answer (click to Show/Hide)

y = 104
Solve: $\frac{n}{5} = \frac{16}{20}$

Answer (click to Show/Hide)

n = 4
Solve: $\frac{39}{c} = \frac{13}{8}$

Answer (click to Show/Hide)

c = 24
The nutrition information for a Caramel Macchiato at Ike’s coffee shop shows that a 16 oz. medium size has 240 calories. How many calories are in a the large size which has 20 oz?

Answer (click to Show/Hide)

300 calories
A Type I diabetic must keep track of the carbs they eat to determine the amount of insulin to give for that meal. For a small eegee that is 6 oz it is estimated there are 18 carbs in the drink. How many carbs are in a 16 oz eegee?

Answer (click to Show/Hide)

48 carbs in 16 oz eegee.
A crepe recipe calls for 2 eggs, 1 cup of flour, and 1 cup of milk. How much flour would you need if you use 5 eggs?

Answer (click to Show/Hide)

2.5 cups
An 8ft length of 4 inch wide crown molding costs $14. How much will it cost to buy 40ft of crown molding?

Answer (click to Show/Hide)

Let “x” be the cost for 40 feet of crown molding. We can assume that the price per foot of 8 ft is the same as 40 ft.

$\begin{array}{l} \frac{$ 14}{8 f t} = \frac{x}{40 f t} \\ x = \frac{$ 14}{8 f t} * 40 f t \\ x = $ 70 \end{array}$
Four 3-megawatt wind turbines can supply enough electricity to power 3000 homes. How many turbines would be required to power 55,000 homes?

Answer (click to Show/Hide)

74 turbines (when rounded up as we can’t have a partial turbine)
A highway had a landslide, where 3,000 cubic yards of material fell on the road, requiring 200 dump truck loads to clear. On another highway, a slide left 40,000 cubic yards on the road. How many dump truck loads would be needed to clear this slide?

Answer (click to Show/Hide)

2667 Trucks (when rounded up as we can’t have a partial truck)
A biologists wants to approximate the number of fish in a lake. Instead of trying to catch all the fish by dragging nets it is easier (and safer for the fish to avoid the stress) to make small catches at different parts of the lake. When doing this on the first day they caught and tagged 102 fish. Two weeks later they go out to the lake and catch 84 fish and 6 of those are tagged. Estimate the total number of fish in the lake.

Answer (click to Show/Hide)

1428 fish
On a map, San Francisco, Las Vegas, and Los Angeles form a triangle whose sides are shown in the figure below. The actual distance from Los Angeles to Las Vegas is 270 miles. Find the distance from Los Angeles to San Francisco.

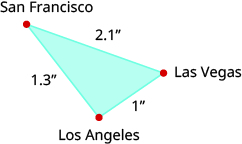
Answer (click to Show/Hide)

351 miles
Determine the missing lengths on the similar triangles.

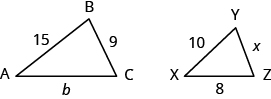
Answer (click to Show/Hide)

b=12 and x=6
Determine the missing lengths on the similar triangles.

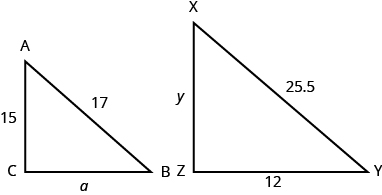
Answer (click to Show/Hide)

a = 8 and y = 22.5

Attributions

This page contains modified content from David Lippman, “Math In Society, 2nd Edition.” Licensed under CC BY-SA 4.0.
This page contains modified content and images from “OpenStax PreAlgebra” by Lynn Marecek, MaryAnne Anthony-Smith. Licensed under CC BY-NC 4.0 / A derivative from the original work
This page contains modified content and images from “Contemporary Mathematics” by Donna Kirk and is licensed under CC BY-NC 4.0 / A derivative from the original work.
This page contains content by Robert Foth, Math Faculty, Pima Community College, 2021. Licensed under CC BY 4.0.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Proportions

Solve Proportions

Solution

Solution

Solve Application Problems Involving Proportions

To determine when you can use a proportional equation

Solution

Solution

Solution

Errors Using Proportional Equations

Examples of Non-Proportional Relationships

Solution

Solution

Solve Application Problems Involving Similar Triangles

Solution

Solution

Exercises

Attributions

License

Share This Book