1.1 Problem-Solving Process

An number of random, simple math equations and geometric diagrams superimposed on top of office workers standing around an office.

1.1: Problem-Solving

Learning Objectives

Upon completion of this section, you should be able to

  • Identify Steps in the Problem-Solving Process
  • Apply Problem-Solving Strategies to Applications

Problem-Solving Process and Strategies

People face multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough. Sometimes, however, the problems we encounter are more complex (where more variables are involved): To determine how far the car can still travel on a quarter tank of gas (this becomes more complex as you consider the fuel efficiency of the vehicle at different speeds).

It is important to start your approach to math and problems with the right attitude. Have you had any thoughts like the ones shown below?

A cartoon image of a girl with a sad expression writing on a piece of paper is shown. There are 5 thought bubbles. They read, “I don't know whether to add, subtract multiply, or divide!,” then “I don't understand word problems!,” then “My teachers never explained this!,” then “If I just skip all the word problems, I can probably still pass the class,” and lastly, “I just can't do this!”

When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.

Start with a fresh slate and begin to think positive thoughts like the student shown below. Read the positive thoughts and say them out loud.

A cartoon image of a girl with a confident expression holding some books is shown. There are 4 thought bubbles. They read, “While word problems were hard in the past, I think I can try them now,” then “I am better prepared now. I think I will begin to understand word problems,” then “I think I can! I think I can!,” and lastly, “It may take time, but I can begin to solve word problems.”

If we take control and believe we set our mind to be more successful.

Think of something that you can do now but couldn’t do three years ago. Whether it’s driving a car, snowboarding, cooking a gourmet meal, or speaking a new language, you have been able to learn and master a new skill.

In many problems, it is tempting to take the given information and plug it into whatever formulas you have handy. Chances are, this approach has served you well in other math classes. This approach does not work well with real life problems as there may be more information given than needed to find the answer you are looking for.  Instead, problem-solving is best approached by first starting at the end: identifying exactly what you are looking for.  From there, you then work backwards, asking “what information and procedures will I need to find this?”

Very few interesting questions can be answered in one mathematical step; often times you will need to chain together a solution pathway, a series of steps that will allow you to answer the question. As we progress through this textbook you will be given opportunities to practice on one step problems and then continue to more complicated and interesting questions where you may need to piece together multiple steps and strategies to find the solution.

Problem-Solving Process

  1. Understand the Problem
  2. Devise a Plan
  3. Carry out the Plan
  4. Look Back

A problem-solving strategy is a plan of action used to find a solution and incorporates the steps from the process. Different strategies have different action plans associated with them. Most of the problem-solving strategies you have seen are built upon a standard foundation that Polya wrote down in his well known book “How to Solve It”. An excerpt is shown below.

Summary taken from G. Polya, “How to Solve It”, 2nd ed., Princeton University Press, 1957, ISBN 0-691-08097-6.

  1. UNDERSTANDING THE PROBLEM
    • First. You have to understand the problem.
    • What is the unknown? What are the data? What is the condition?
    • Is it possible to satisfy the condition? Is the condition sufficient to determine the unknown? Or is it insufficient? Or redundant? Or contradictory?
    • Draw a figure. Introduce suitable notation.
    • Separate the various parts of the condition. Can you write them down?
  2. DEVISING A PLAN
    • Second. Find the connection between the data and the unknown. You may be obliged to consider auxiliary problems if an immediate connection cannot be found. You should obtain eventually a plan of the solution.
    • Have you seen it before? Or have you seen the same problem in a slightly different form?
    • Do you know a related problem? Do you know a theorem that could be useful?
    • Look at the unknown! And try to think of a familiar problem having the same or a similar unknown.
    • Here is a problem related to yours and solved before. Could you use it? Could you use its result? Could you use its method? Should you introduce some auxiliary element in order to make its use possible?
    • Could you restate the problem? Could you restate it still differently? Go back to definitions.
    • If you cannot solve the proposed problem try to solve first some related problem. Could you imagine a more accessible related problem? A more general problem? A more special problem? An analogous problem? Could you solve a part of the problem? Keep only a part of the condition, drop the other part; how far is the unknown then determined, how can it vary? Could you derive something useful from the data? Could you think of other data appropriate to determine the unknown? Could you change the unknown or data, or both if necessary, so that the new unknown and the new data are nearer to each other?
    • Did you use all the data? Did you use the whole condition? Have you taken into account all essential notions involved in the problem?
  3. CARRYING OUT THE PLAN
    • Third. Carry out your plan.
    • Carrying out your plan of the solution, check each step. Can you see clearly that the step is correct? Can you prove that it is correct?
  4. Looking Back
    • Fourth. Examine the solution obtained.
    • Can you check the result? Can you check the argument?
    • Can you derive the solution differently? Can you see it at a glance?
    • Can you use the result, or the method, for some other problem?

Many corporations and militaries have studied problem-solving strategies and they all have similarities to the summary listed about in Polyas book (first published in 1945). These four steps should act as a guideline to any problem you see and come across.

In the list above from Poyla the first step of “understand the problem” is the most important. If you don’t understand the problem you are dealing with, then it will be hard to figure out a solution. To help understand the problem we can employ multiple strategies to get familiar with what is being asked. Depending on the circumstances of the problem you can try visualizing the situation by drawing a diagram, if it represents a game try playing the game for a short period to become familiar with how it works and what possible outcomes there may be. If there are words you are unfamiliar with use a dictionary to find out what they mean as it might shed light on details you were not aware of. Each of these may lead to something unexpected in helping understand the problem.

In regards to devising a plan there are many different approaches you can take and there may not be just one to help you. The table below gives some ideas to help get started on that step for problem-solving.

1. Guess and test. 11. Solve an equivalent problem.
2. Use a variable. 12. Work backwards
3. Draw a picture. 13. Use cases.
4. Look for a pattern. 14. Solve an equation.
5. Make a list. 15. Look for a formula.
6. Solve a simpler problem. 16. Do a simulation.
7. Draw a diagram. 17. Use a model
8. Use direct reasoning.

In a textbook we often simplify the real life situations down to single step problems in order to give learners an opportunity to practice some new concept or formula. I have to agree with Dan Meyer (see his talk below – also the author of dy/dan blog) that some of these textbook contrived examples do not work well in teaching problem-solving when not all the details are provided, but they do help by introducing the new concept or skill to build up a better toolbelt of strategies and knowledge to work from. If you plan on going into teaching as a career (or plan on having kids whom you will be teaching) you should watch the video below.

Video Source: https://www.ted.com/talks/dan_meyer_math_curriculum_makeover

Math class needs a makeover (11 min 40 sec CC)

One last thing before we look at some examples is about estimation. In many problems you will be approximating a solution, because we will not have perfect information and will need to make some assumption to move forward. For instance if you had a quarter tank of gas left you tend to estimate how much farther you can go (maybe that quarter tank was an estimate as well) before having to fuel up. You may be estimating how long it will take you to get to work or school from the time you leave home. This type of estimating is based on your previous knowledge and experiences in similar circumstances. What we want to look at is something similar, but with a focus on estimating values for some mathematical computation and relation.

What we will not discuss about estimation.

We are not going to discuss how we are hardwired to deceive ourselves when estimating, which is a fascinating topic and large amount of material has been written about, but not related to what we want to use estimation for (watch this presentation by Linda Rising 1 hour and 33 mins – CC if this interests you). It is worth knowing that people do have misconceptions and are typically very bad estimators of outcomes of an event without using data (did you know over 80% of truck drivers believe they are above average? This is an example of illusory superiority)

We will begin with a few examples where we will be able to approximate the solution using basic knowledge from our lives.

Example 1

Estimate how many times does your heart beat in a year?

Solution

  1. Understand the Problem. This question is straight forward in wanting the number of heartbeats in a single year. A brute force approach of counting your heartbeat for an entire year does not seem reasonable for an approach, so we need to determine a different approach.
  2. Devise a Plan. We could start with an easier problem and see if this can be expanded to find our solution (this is often a good strategy to help with understanding the problem as well). A simpler problem may be how many heartbeats are in a minute? To answer this question we could look for data about the number of heartbeats in a minute online through a reputable source or you could estimate this number by counting your own number of heartbeats in a minute. Either approach allows us to find a direct answer to that easier question.Let’s assume we counted the number of heartbeats and had a result of 80 heartbeats per minute. How does this help us with the larger problem of finding out heartbeats in a year? If we count the number of minutes in a year we could estimate the number of heartbeats in a year by multiplying 80 by that number. That smaller problem gave us the first piece for solving the larger problem.
  3. Carry out the Plan. There are 365 days for a typical year. In a day there are 24 hours. In an hour there are 60 minutes. Putting this all together we can find the number of minutes in a year:
    365 (days/year)*24(hours/day)*60(minutes/hour) = 525,600 minutes for a year.
    The estimate for the number of heart beats in a single year would be 80 * 525,600 = 42,048,000
  4. Looking Back. We could search to see if this estimate matches up with what you can find from reputable sources on the internet. From the American Heart Association we can find information that a normal heart rate is between 60 to 100 beats per minute. Our estimate of 80 seems to be right in the middle and that portion of the work agrees with our findings at All About Heart Rate (Pulse). Assuming our strategy is correct we would have a good estimate for the number of heart beats in a year. We did however assume the heart rate was constant throughout a day, so the actual value may be different for an individual based on other factors like exercise and sleep as both change the heart rate for an individual.

Video Solution (1 min 55 secs – CC). Another example starts after the 1:55 mark of the video.

Example 2

Estimate how thick is a single sheet of 8.5 x 11 inches printer paper. How much does it weigh?

Solution

  1. Understand the Problem. This is another problem that seems straight forward until you try to measure the papers width by hand.
  2. Devise a Plan. Instead of directly measuring a single piece of paper we might try a stack of paper instead, and then scale the thickness and weight to a single sheet. It may be easy to get the information for a ream of paper from an online store and use that information to then estimate the thickness and weight of a single sheet. One ream of paper (500 sheets) found on an online stores website shows that the thickness of the ream is about 2 inches and weighs about 5 pounds.
  3. Carry out the Plan. Using the information we found from the store we can determine the thickness and weight by dividing the amount for the ream by 500, since there were 500 sheets of paper in the ream.

    2inchesream⋅1ream500pages=0.004inches per sheet

    5poundsream⋅1ream500pages=0.01pounds per sheet, or 0.16 ounces per sheet.

  4. Looking Back. You can check thickness of most reams of paper directly on the package. A typical sheet has a thickness of roughly .1 mm and our estimate we found matches up when converting millimeters to inches.

Video Solution (approximately 2 mins – CC)

Example 3

A recipe for zucchini muffins states that it yields 12 muffins, with 250 calories per muffin. You decide to make the exact same recipe, but instead make 20 mini-muffins. If the amount of ingredients is exactly the same, then how many calories would 4 of the mini-muffins be?

Solution

  1. Understand the Problem. We need to find how many calories it is for 4 mini-muffins from the same recipe that created 12 muffins with each muffin being 250 calories.
  2. Devise a Plan. To answer the question of how many calories 4 mini-muffins will contain, we would want to know the number of calories in each mini-muffin. Since both batches (the 12 muffins and 20 mini-muffins) have the same ingrediants they should both have the same total calories for all their respective amount of muffins. To find the calories in each mini-muffin, we could take the total calories for the entire recipe, then divide it by the number of mini-muffins produced. To find the total calories for the recipe, we could multiply the calories per standard muffin (12 muffin batch) by 12 (the number of muffins).  Notice that this produces a multi-step solution pathway.  It is often easier to solve a problem in small steps, rather than trying to find a way to jump directly from the given information to the solution.
  3. Carry out the Plan.

    12muffins⋅250caloriesmuffin=3000calories for the whole recipe

    3000calories20mini-muffins=150caloriesmini-muffins, or 150 calories per mini-muffin

    4mini-muffins⋅150 caloriesmini-muffins=600calories consumed

  4. Looking Back. One way to see if our result seems reasonable is to check to see if things seem realistic. Since the 20 mini-muffin batch would be spreading out the calories to more muffins we should expect to see the number of calories per muffin to be smaller when compared to the 12 muffin batch. The 12 muffin batch had 250 calories per muffin while the 20 mini-muffin batch had 150 calories per muffing. This fits our expectations and helps us feel more confident in the final result being correct or at least in the right direction.

Video Solution (4 mins 1 sec – CC).

In the next examples solution we will explore another strategy that can help explore the problem while also providing a solution. It uses the Guess and Test method where through an iteration of trials you approach the solution or come up with a strategy based on finding to answer the question.

Example 4

A farmer has a total of 20 chickens and cows on his farm. How many of each does he have if all together there are 52 feet?

Solution

  1. Understand the Problem. The details we need involve the total number of chicken and cows to add up to 20 and when counting the feet a total of 52 is present. Each chicken is assumed to only have two feet and each cow would have four feet.
  2. Devise a Plan. It may help to start with dividing the 20 animals into 10 chickens and 10 cows and explore how many feet you would find with that division. With 10 chickens there are 20 feet (each chicken has two feet) and with 10 cows we would have 40 feet (each cow has four feet). To help organize our work inserting the information in a table and gradually changing values may help identify how to update each new guess.
  3. Carry out the Plan. Start with putting the first results of 10 chickens and 10 cows and add one more row where you add one more cow and one less chicken to see how things change.
    Number of chickens Number of cows Number of chicken feet Number of cow feet Total number of feet
    10 10 20 40 60
    9 11 18 44 62

    Now looking over what happened is that when we updated the number of cows to one more the total number of feet went up. This is heading us in the wrong direction as we wanted to find a total of 52 feet which is less than the 60 feet we had when there were 10 chickens and 10 cows. Lets continue guessing by moving in the other direction (decrease the number of cows and increase the number of chickens).

    Number of chickens Number of cows Number of chicken feet Number of cow feet Total number of feet
    10 10 20 40 60
    11 9 22 36 58
    12 8 24 32 56
    13 7 26 28 54
    14 6 28 24 52

    In the last row we see that we found the correct number. With 14 chickens and 6 cows there are a total of 52 feet.

  4. Lookin Back. Now this time around we used a guess and check approach and then adjusted values to determine what to do next. When raising the number of cows we saw the total feet go up (which makes sense as cows have two more feet than chickens). This strategy is good when there are more limited number of choices to go between. If we had more choices we could update the strategy by changing our guess by larger jumps and applying more logic on the guess based on the situation.

The Problem-Solving Process outlined in this section gives you a framework to approach problems not just in your mathematics courses. This process is to help you break apart a problem into pieces to help explore what you are working on. As mentioned earlier the mathematics course you are taking that goes along with this text will introduce simple problems where a single step is needed to help you practice on a particular skill or concept, but as you progress you will run into multi-step problems that require you to build out a solution pathway that may take multiple iterations to fine tune. Using the problem-solving process can help in identifying what you are trying to answer.

Exercises

In the next 2 questions, estimate the values by making reasonable approximations for unknown values, or by doing some research to find reasonable values.

  1. Estimate how many gallons of water you drink in a year.
  2. Estimate how many times you blink in a day.
  3. Samantha offers to buy 10 lipsticks from Luz. Luz says she can pay $200 for all 10 lipsticks, or she can give her 50¢ for the first lipstick, $1 for the next, $2 for the third, and continuing so each lipstick costs twice what the previous lipstick cost. Which payment should Samantha choose?
  4. List the ways you can make change for $50 using only $5, $10, and $20 bills. For instance, one way is 20, 10, 5, 5, 5, 5.
  5. Soda is often sold in 20 ounce bottles. The nutrition label for one of these bottles is shown below. A packet of sugar (the kind they have at restaurants for your coffee or tea) typically contain 4 grams of sugar in the U.S. Drinking a 20 oz soda is equivalent to eating how many packets of sugar?
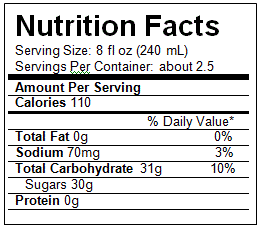
    Text Box: Nutrition Facts Serving Size: 8 fl oz (240 mL) Servings Per Container: about 2.5 Amount Per Serving Calories 110 % Daily Value* Total Fat 0g 0% Sodium 70mg 3% Total Carbohydrate 31g 10% Sugars 30g Protein 0g
  6. Brandon walked from Rincon/UHS to UofA. It took him 1 hour and 35 minutes. He then took 45 minutes to walk from UofA to Pima Downtown Campus. If he did not stop at any point and arrived at the Pima Downtown Campus at 4:25 pm, then what time did he leave Rincon/UHS?
  7. Abby is not a morning person and needs to plan on what time to wake up for a morning class. She needs 30 minutes to get ready in the morning. It takes her 25 minutes to bike to campus and walk to class. If her class starts at 8:45 a.m. what time should she set her alarm for?

Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Topics in Mathematics Copyright © by Robert Foth is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book