1.4 Dimensional Analysis

1.4: Dimensional Analysis
Learning Objectives
Upon completion of this section, you should be able to
- Solve problems using rates.
- Convert between common measurements.
- Solve application problems involving conversion of units.
Rates
In the last section we introduced the definition of a rate. Remember a rate is a comparison of two quantities with different units, such as miles per gallon, words per minute, or dollars per ounce. In many applications we may not need to go to the step of writing a proportion equation if we are given a rate.
Rate and Unit Rate
A rate compares two quantities of different units.
A unit rate is a rate with a denominator of one.
When writing a fraction as a rate, we put the first given amount with its units in the numerator and the second amount with its units in the denominator. When rates are simplified, the units remain in the numerator and denominator. For example if Darla drove her car 525 miles in 10 hours we can express this information as a rate or as as a unit rate.
The advantage of a unit rate is that if we multiply that unit rate by the amount of time (in hours) we will get the distance traveled in that time. This removes a step in setting up a proportion equation to solve. This strategy of multiplying the rate by the known quantity can be used as long as we make sure to have the unit rate denominator be the same units as what we are multiplying by (as we will see in the next example).
Example 1
Your car can drive 300 miles on a tank of 15 gallons. Express this as a rate and a unit rate.
Solution
Expressed as a rate: .
We can divide 15 into 300 to find a unit rate: .
We could also write as , or just 20 miles per gallon.
Video Solution (1 min 3 secs - CC) Another example starts after the 1:03 mark of the video.
Many problems involving rates can be solved by using dimensional analysis, the process of multiplying a quantity by rate(s) to change the units. For example if we know that a car is traveling at a constant rate of 60 miles per hour and travels for 3 hours we can find the distance traveled by multipling the rate by the time to find that the car traveled 180 miles. This process leads us to the general formula for distance traveled (D) over time (T) with a constant rate (R) as . One caution with using the formula is that the rate and time must be using the same units of time. We will see how to handle the situation when they are not the same units in a later example.
Dimensional Analysis
Dimensional analysis is a method to convert one kind of unit to another.
Example 2
Your car can drive 300 miles on a tank of 15 gallons. How far can it drive on 40 gallons?
Solution
We could certainly answer this question using a proportion:
However, we earlier found that 300 miles on 15 gallons gives a rate of 20 miles per gallon. If we multiply the given 40 gallon quantity by this rate, the gallons unit “cancels” and we’re left with a number of miles:
The car would be able to drive 800 miles on 40 gallons.
Notice if instead we were asked “how many gallons are needed to drive 50 miles?” we could answer this question by inverting the 20 mile per gallon rate so that the miles unit cancels and we’re left with gallons:
Video Solution(4 mins 12 secs - CC)
Unit prices are very useful if you comparison shop. The better buy is the item with the lower unit price. Most grocery stores list the unit price of each item on the shelves.
Example 3
Paul is shopping for laundry detergent. At the grocery store, the liquid detergent is priced at $14.99 for 64 loads of laundry and the same brand of powder detergent is priced at $15.99 for 80 loads.
Which detergent has the lowest cost per load?
Solution
To compare the prices, we first find the unit price for each type of detergent.
| Liquid | Powder | |
|---|---|---|
| Write as a rate. | ||
| Find the unit price. | ||
| Round to the nearest cent. |
Now we compare the unit prices. The unit price of the liquid detergent is about $0.23 per load and the unit price of the powder detergent is about $0.20 per load. The powder is the better buy.
Try it Now 1
Albert’s Honda Civic gets 37 miles per gallon of gasoline. The gas tank on the Civic can hold 13.5 gallons of gas. Albert is driving from Tucson, Arizona to Los Angeles, California, a distance of 485 miles. Albert thinks he can make it on one full tank of gasoline. Can he?
Answer (click to Show/Hide)
If we multiply the 13.5 gallons by the rate 37 miles per gallon the gallon units would cancel out and we are left with the distance traveled in miles.
Yes he can, but barely. At 37 miles per gallon, Albert can drive 499.5 miles. While in theory he can make it, he probably should fill up with gasoline somewhere along the way!
Convert Between Common Measurements
You will often encounter situations where converting between different units of measurement is necessary. This is where dimensional analysis becomes a powerful tool. While most countries around the world use the Metric system, the United States primarily uses a different system known as the United States customary units. This system is sometimes referred to as English Units or the Imperial System, although it's worth noting that even England now uses the metric system.
You might be surprised to learn that the metric system is already a significant part of daily life in the United States. Even though we still buy milk by the gallon and measure house sizes in square feet, metric units are more common than you might think. Here are some examples:
- Soda is often sold in 2-liter bottles
- Medicine dosages are typically measured in milligrams or milliliters
- Athletes run 100-meter dashes in track events
- Car engine sizes are usually given in liters
- Ammunition is often described using metric calibers (e.g., 9mm)
- Scientific measurements almost always use metric units
Understanding how to convert between these two systems is crucial, whether you're traveling abroad, pursuing a career in science or engineering, or simply trying to understand product specifications. In the following sections, we'll explore various conversion techniques and practice problems to help you master this essential skill.
In the video, Neil DeGrasse Tyson and comedian co-host Chuck Nice provide an amusing perspective on the metric system. Neil deGrasse Tyson Explains the Metric System
Here are some unit conversions for reference that has both the Metric system and US system. If you plan on traveling outside of the US you will most likely see measurements given in the metric system.
Unit Conversions
| Length | Volume |
|---|---|
|
1 foot (ft) = 12 inches (in) 1 yard (yd) = 3 feet (ft) 1 mile (mi) = 5,280 feet (ft) 1000 millimeters (mm) = 1 meter (m) 100 centimeters (cm) = 1 meter (m) 1000 meters (m) = 1 kilometer (km) 2.54 centimeters (cm) = 1 inch (in) |
1 tablespoon (tbsp) = 3 teaspoon (tsp) 1 cup (C) = 16 tablespoons (tbsp) 1 cup (C) = 8 fluid ounces (fl oz) 1 pint (pt) = 2 cups (C) 1 quart (qt) = 2 pints (pt) 1 gallon (gal) = 4 quarts 1000 milliliters (ml) = 1 liter (L) 1 gallon = 0.134 cubic ft |
| Weight and Mass | Time |
|---|---|
|
1 pound (lb) = 16 ounces (oz) 1 ton = 2000 pounds (lb) 1000 milligrams (mg) = 1 gram (g) 1000 grams (g) = 1kilogram (kg) 1 kilogram (kg) = 2.2 pounds (lb) (on earth) |
1 minute (min) = 60 seconds (s) 1 hour (h) = 60 minutes (min) 1 day = 24 hours (h) 1 week (wk) = 7 days 1 year (yr) = 365 days |
In many real-life applications, we need to convert between units of measurement. We will use the identity property of multiplication to do these conversions. We’ll restate the Identity Property of Multiplication here for easy reference.
To use the identity property of multiplication, we write 1 in a form that will help us convert the units. For example, suppose we want to convert inches to feet. We know that 1 foot is equal to 12 inches, so we can write 1 as the fraction . When we multiply by this fraction, we do not change the value but just change the units.
But also equals 1. How do we decide whether to multiply by or ? We choose the fraction that will make the units we want to convert from divide out. For example, suppose we wanted to convert 60 inches to feet. If we choose the fraction that has the inches in the denominator, we can then eliminate the inches.
On the other hand, if we wanted to convert 5 feet to inches, we would choose the fraction that has feet in the
denominator.
We treat the unit words like factors and 'divide out' common units like we do common factors.
- Multiply the measurement to be converted by 1; write 1 as a fraction relating the units given and the units needed.
- Multiply.
- Simplify the fraction, performing the indicated operations and removing the common units.
Example 4
Convert each of the following to the units given.
- 12 cm to inches
- 48 oz to pounds
- 3 quarts to ounces
- 20 yds to meters
Solution
For 1 and 2 we can directly convert the values from the table with one ratio. When you examine 3 and 4 we don't see these two values directly related on the table. To find the conversion you connect relations until you have a path between the units to be converted.
1. The table gives the relation between cm and inches as 2.54 centimeters (cm) = 1 inch (in)
2. The table gives the relation between oz to lbs as 1 pound (lb) = 16 ounces (oz).
3. To convert from quart to ounces this is another example of having to build a road map between those units on the given values. From the table we can go from quarts to pints, pints to cups, and then cups to ounces.
4. To convert from yd to meters a road map needs to be built to get from yd to meters from the table of values given. We can go from yards to feet, feet to inches, inches to cm, and then cm to meters.
In some situations we are dealing with units that are squared or cubed if the application is involving area or volume. In those cases we treat an area unit like ft2 as the units of feet times itself or feet*feet and will need a conversion for each one in order to find the new units we are looking for.
Example 5
Convert each of the following to the units given.
- 45 ft2 to yd2
- 2 m3 to cm3
Solution
1. To start we identify that the squared feet unit is actually feet*feet and will need to remove it twice with a conversion formula.
2. Treat the cubic meters as meters*meters*meters and then convert each meter unit to centimeters.
Lets take a look at an application that has mixed units now.
Example 6
A bicycle is traveling at 15 miles per hour. How many feet will it cover in 20 seconds?
Solution
This is very similar to a problem we did before where we can use the formula to solve.
To answer this question, however, we need to convert 20 seconds into hours so that we are dealing with the same units in time for both pieces of information given. If we know the speed of the bicycle in feet per second, this question would be simpler. Since we don’t, we will need to do additional unit conversions. We might start by converting the 20 seconds into hours and then deal with converting the miles into feet:
We could have also done this entire calculation in one long set of products by using the formula D=R*T and
doing the unit conversions in the work all at once:
Video Solution (4 mins 4 secs - CC)
Try it Now 2
A 1000 foot spool of bare 12-gauge copper wire weighs 19.8 pounds. How much will 18 inches of the wire weigh, in ounces?
Hint 1 (click to Show/Hide)
Before you try to set up a proportional equation we have to determine if we are comparing apples to apples or apples to oranges (are the units the same for each proportion we set up?)
Hint 2 (click to Show/Hide)
Convert the length to inches and the weight to ounces before you start.
1 ft = 12 inches
16 ounces = 1 pound
Answer (click to Show/Hide)
Convert the length to inches and the weight to ounces before you start.
Length:
Weight:
Setup the proportion to relate the length and weights that have the same units, where x is the unknown weight for the 18 inches of wire.
Now solve for x
The 18 inches of wire will weight 0.4752 ounces.
Further Applications With Unit Conversions
Many geometry applications will involve finding the perimeter or the area of a figure. There are also many applications of perimeter and area in everyday life, so it is important to make sure you understand what they each mean.
Picture a room that needs new floor tiles. The tiles come in squares that are a foot on each side—one square foot. How many of those squares are needed to cover the floor? This is the area of the floor.
Next, think about putting new baseboard around the room, once the tiles have been laid. To figure out how many strips are needed, you must know the distance around the room. You would use a tape measure to measure the number of feet around the room. This distance is the perimeter.
Perimeter and Area
The perimeter is a measure of the distance around a figure.
The area is a measure of the surface covered by a figure.
It may be helpful to recall some formulas for areas and perimeter of a few basic two dimensional shapes.
Two Dimensional Shapes
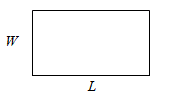
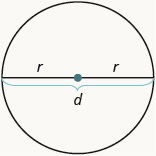
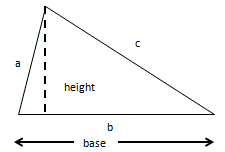
| Rectangle | Circle | Triangle |
|---|---|---|
|
|
r is the length of the radius and is the length of the diameter. We call the circumference the length of the perimeter.
|
|
Example 7
A circular shaped sandbox is to be constructed from bricks that are (or 7.625 in) long. The diameter of the sandbox was measured to be 12 ft. How many bricks should be purchased if we assume the brick when laid out is approximately a circular shape?
Solution
The circumference of a circle represents the total distance around a circle. We can use the circumference formula to find a rough estimate for that total distance and then use that information to determine how many bricks to purchase. It would be appropriate to round the answer up as it is unlikely to be able to purchase a portion of a brick when going to a store.
The circumference was found to be roughly 37.7 ft. Now to find how many bricks are needed we can use division, but with the units not matching we should first change the circumference into inches.
Divide the circumference by the length of the brick, 7.625 inches.
Rounding up leaves us with needing 60 bricks needed for the cirular sandbox.
The rectangular solid shown in the Figure below has length 4 units, width 2 units, and height 3 units. Can you tell how many cubic units there are altogether? Let’s look layer by layer.
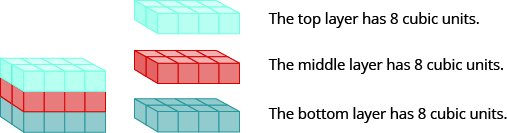
Breaking a rectangular solid into layers makes it easier to visualize the number of cubic units it
contains. This 4 by 2 by 3 rectangular solid has 24 cubic units.
Altogether there are 24 cubic units. Notice that 24 is the length×widthxheight.
The volume, V, of any rectangular solid is the product of the length, width, and height.
We could also write the formula for volume of a rectangular solid in terms of the area of the base. The area of the base, B, is equal to length×width.
We can substitute B for L·W in the volume formula to get another form of the volume formula.
We now have another version of the volume formula for rectangular solids. Let’s see how this works with the 4×2×3 rectangular solid we started with.
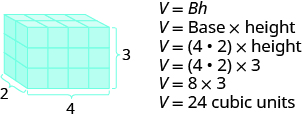
Volume of the rectangular solid is the area of the base multiplied by the height.
To find the surface area of a rectangular solid, think about finding the area of each of its faces. How many faces does the rectangular solid above have? You can see three of them.
Notice for each of the three faces you see, there is an identical opposite face that does not show.
The surface area S of the rectangular solid shown in Figure above is 52 square units.
In general, to find the surface area of a rectangular solid, remember that each face is a rectangle, so its area is the product of its length and its width (see Figure below). Find the area of each face that you see and then multiply each area by two to account for the face on the opposite side.
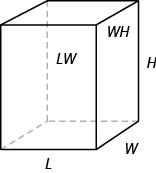
For each face of the rectangular solid facing you, there is another face on the opposite side. There are 6 faces in all.
Three Dimensional
| Rectangular Box | Cylinder |
|---|---|
 |
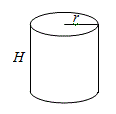 |
Example 8
The local preschool is installing a new sandbox in their outdoor play area. The playground designer has specified the following dimensions for the sandbox:
- Length: 12 feet
- Width: 8 feet
- Depth: 15 inches
The preschool needs to order sand to fill this sandbox. Find the cost to fill this sandbox if 1 cubic yard is sold for $30 (can only purchase by a whole cubic yard).
Solution
Step 1: Convert all dimensions to the same unit (feet)
- Length: 12 feet
- Width: 8 feet
- Depth:
Step 2: Calculate the volume of the sandbox
Step 3: Since the sand is sold in cubic yards we will need to convert our volume in cubic feet of sand to cubic yards
Step 4: Calculate the cost
Rounding up we need to purchase 5 one cubic yard bags of sand.
The preschool will need to pay $150 to purchase 5 cubic yards of sand for the sandbox.
We don't always need to have an exact measurements if there is a way to create our own units to scale items as shown in the next example below.
Example 9
A company makes regular and jumbo marshmallows. The
regular marshmallow has 25 calories. How many calories will the jumbo marshmallow have?

Solution
We would expect the calories to scale with volume. Since the marshmallows have cylindrical shapes, we can use that formula to find the volume. From the grid in the image, we can estimate the radius and height of each marshmallow.
The regular marshmallow appears to have a diameter of about 3.5 units, giving a radius of 1.75 units, and a height of about 3.5 units. The volume is about
.
The jumbo marshmallow appears to have a diameter of about 5.5 units, giving a radius of 2.75 units, and a height of about 5 units. The volume is about
.
We could now set up a proportion, or use rates. The regular marshmallow has 25 calories for 33.7 cubic units of volume. The jumbo marshmallow will have:
It is interesting to note that while the diameter and height are about 1.5 times larger for the jumbo marshmallow, the volume and calories are about 1.53 = 3.375 times larger.
Video Solution (2 mins and 19 seconds - CC)
Exercises
- Find a unit rate: You drove 360 miles on 20 gallons of fuel.
Answer (click to Show/Hide)
A unit rate describes how many units of the first quantity correspond to one unit of the second quantity. Let us find the number of miles per one gallon of fuel. An alternative unit rate is number of gallons per one mile driven. Both represent unit rates.
To find this, we set up a ratio and divide the number of miles by the number of gallons.
Now, perform the division:
Answer: The unit rate is 18 miles per gallon. Alternatively, the rate can be expressed as approximately 0.056 gallons per mile.
- Find a unit rate: You bought 10 pounds of potatoes for $4.
Answer (click to Show/Hide)
A unit rate describes how many units of one quantity correspond to one unit of another quantity. To find the cost per pound, we set up a ratio and divide the total cost by the number of pounds.
Now, perform the division:
Answer: The unit rate is $0.40 per pound. Alternatively, the rate can be expressed as 2.5 pounds per dollar.
- Find a unit rate: Joel ran 1500 meters in 4 minutes, 45 seconds.
Answer (click to Show/Hide)
Let us find the speed in meters per second. Alternatively you could find seconds per 1 meter ran. Both represent a unit rate.
First, we need to convert the total time into a single unit (seconds).
Now we can set up the ratio of meters to seconds.
Finally, perform the division to find the unit rate.
Answer: Joel's unit rate (speed) is approximately 5.26 meters per second. Alternatively, the rate can be expressed as 0.19 seconds per meter.
- Convert 8 feet to inches.
Answer (click to Show/Hide)
To convert units, we can use a conversion factor. We know that 1 foot = 12 inches. We can write this as a fraction. To cancel the "feet" unit, we need it in the denominator of our conversion factor.
We set up the problem by multiplying the original value by the conversion fraction, which allows the "feet" units to cancel out.
Answer: 8 feet is equal to 96 inches.
- Convert 2 miles to yards.
Answer (click to Show/Hide)
To perform this conversion, we can use two conversion factors: one for miles to feet (1 mi = 5280 ft), and one for feet to yards (3 ft = 1 yd).
We will set these up as a series of fractions. The first fraction will convert miles to feet, and the second will convert feet to yards. The units are arranged so that "mi" and "ft" cancel out, leaving "yd" as the final unit.
Answer: 2 miles is equal to 3520 yards.
- Convert 40 miles to kilometers.
Answer (click to Show/Hide)
To solve this, we will create a chain of conversion factors that will take us from miles to kilometers. Each fraction is set up so that the unit in the numerator of the previous term is canceled by the unit in the denominator of the next term.
The conversion factors are: 1 mi = 5280 ft, 1 ft = 12 in, 1 in = 2.54 cm, 100 cm = 1 m, and 1000 m = 1 km.
Answer: 40 miles is equal to approximately 64.37 km.
- Convert 6 kilograms to grams.
Answer (click to Show/Hide)
To perform this conversion, we need the conversion factor between kilograms and grams: 1 kg = 1000 g. We will set this up as a fraction so that the "kg" unit is in the denominator, allowing it to cancel out.
We multiply the original value by this conversion fraction to find the equivalent mass in grams.
Answer: 6 kilograms is equal to 6000 grams.
- Convert 2.5 gallons to ounces.
Answer (click to Show/Hide)
To perform this conversion, we will create a chain of conversion factors to take us from gallons to ounces. The fractions are arranged so that each unit is canceled out by the next one in the chain, leaving only ounces at the end.
The conversion factors are: 1 gal = 4 qt, 1 qt = 2 pt, 1 pt = 2 cups, and 1 cup = 8 oz.
Answer: 2.5 gallons is equal to 320 ounces.
- An outdoor track is 400 m long. If you run 10 laps around the track, how many kilometers have you run?
Answer (click to Show/Hide)
This problem requires two steps. First, we need to calculate the total distance run in meters. Second, we will convert that total distance from meters to kilometers.
Step 1: Calculate the total distance in meters.
We multiply the length of one lap by the number of laps run.Step 2: Convert the total distance to kilometers.
Now, we use the conversion factor 1 km = 1000 m to convert the 4000 m to kilometers. We set up the fraction so the meter unit cancels out.Answer: You have run 4 kilometers.
- An aspirin tablet is 650 mg. If you take 2 aspirin twice in one day, how many grams of aspirin have you taken?
Answer (click to Show/Hide)
This problem requires two steps. First, we need to calculate the total amount of aspirin taken in milligrams (mg). Second, we will convert that total amount from milligrams to grams (g).
Step 1: Calculate the total dosage in milligrams.
You take 2 tablets, two times a day, which is a total of 4 tablets. We multiply the number of tablets by the dosage per tablet.Step 2: Convert the total dosage to grams.
Now, we use the conversion factor 1 g = 1000 mg to convert the 2600 mg to grams. We set up the fraction so the milligram unit cancels out.Answer: You have taken 2.6 grams of aspirin.
- A wire costs $2 per meter. How much will 3 kilometers of wire cost?
Answer (click to Show/Hide)
This problem requires two steps since the units for the length of the wire does not match the units of cost. First, we need to convert the length of the wire from kilometers (km) to meters (m). Second, we will use the cost per meter to find the total cost for the entire length of wire.
Step 1: Convert the length from kilometers to meters.
We use the conversion factor 1 km = 1000 m. We set up the fraction so the kilometer unit cancels out.Step 2: Calculate the total cost.
Now, we multiply the total length in meters by the cost per meter. We set up the fraction so the meter unit cancels out, leaving only the cost.Answer: 3 kilometers of wire will cost $6,000.
- Sugar contains 15 calories per teaspoon. How many calories are in 1 cup of sugar?
Answer (click to Show/Hide)
This problem requires a multi-step unit conversion. We will start with the known rate of calories per teaspoon and use the conversion factors to find the calories per cup. The standard conversions are 3 teaspoons (tsp) = 1 tablespoon (tbsp), and 16 tablespoons (tbsp) = 1 cup.
We can set up a single calculation where the units cancel out, leaving us with calories per cup.
Now we multiply the numbers to find the final result.
Answer: There are 720 calories in 1 cup of sugar.
- A car is driving at 100 kilometers per hour. How far does it travel in 2 seconds (in meters)?
Answer (click to Show/Hide)
We will use the fundamental formula for distance: Distance = Rate × Time (D = RT). To solve this, we first need to make sure the units for Rate and Time are consistent before we can multiply them. The final answer for the distance needs to be in meters.
Step 1: Identify the given Rate and Time.
Rate (R): 100 kilometers per hour (km/hr)
Time (T): 2 seconds (s)
As you can see, the rate is in hours, but the time is in seconds. We must convert the rate to units that are compatible with seconds. Since we want the final distance in meters, we will convert the rate from kilometers per hour (km/hr) to meters per second (m/s).
Step 2: Convert the Rate to meters per second (m/s).
We use the conversion factors: 1 km = 1000 m, 1 hour = 60 minutes, and 1 minute = 60 seconds.Step 3: Calculate the Distance.
Now that the rate is in meters per second, we can use the formula D = RT.Answer: The car travels approximately 55.56 meters in 2 seconds.
- A chain weighs 10 pounds per foot. How many ounces will 4 inches weigh? Round your answer to the nearest tenth of an ounce.
Answer (click to Show/Hide)
To solve this, we first need to convert the rate of weight from pounds per foot to ounces per inch. Once we have that rate, we can multiply it by the given length (4 inches) to find the final weight in ounces.
The necessary conversions are: 1 foot = 12 inches, and 1 pound = 16 ounces.
Step 1: Convert the Rate to ounces per inch (oz/in).
We start with the given rate and use the conversion factors to change the units.Step 2: Calculate the total weight for 4 inches.
Now that we have the rate in ounces per inch, we can find the weight of 4 inches of the chain.Answer: 4 inches of the chain will weigh approximately 53.3 ounces.
- A recipe for sabayon calls for 2 egg yolks, 3 tablespoons of sugar, and ¼ cup of white wine. After cracking the eggs, you start measuring the sugar, but accidentally put in 4 tablespoons of sugar. How can you compensate? Hint you will also need to consider the reality of not being able to accurately measure a portion of a yolk and standard measuing cup sizes.
Answer (click to Show/Hide)
The key is to maintain the original ratio of ingredients. Since you've used more sugar than the recipe calls for, you'll need to increase the other ingredients proportionally.
Step 1: Find the scaling factor.
First, we determine by what factor the amount of sugar has increased.This means we need to scale up all other ingredients by a factor of 4/3 to keep the recipe balanced.
Step 2: Calculate the new total amounts for the other ingredients.
Now, we multiply the original amounts of egg yolks and wine by the scaling factor.New Egg Yolks:
New White Wine:
Step 3: Adjust for Practical Measurements.
The calculation shows we need a total of 2 2/3 egg yolks, which is not practical for a cook. We should scale the recipe up to the next whole egg yolk, which is 3. To do this, we find a new scaling factor based on the egg yolks.Step 4: Recalculate all ingredients with the new, practical factor.
We will now make a larger batch that uses 3 whole egg yolks.Total Sugar Needed:
Total Wine Needed:
Step 5: Determine how much more to add.
We compare what we need for the practical batch to what's already in the bowl (2 yolks, 4 tbsp sugar, 1/4 cup wine).Egg Yolks to Add: 3 (needed) - 2 (have) = 1 whole yolk
Sugar to Add: 4.5 tbsp (needed) - 4 tbsp (have) = 0.5 tbsp (or 1/2 tbsp)
Wine to Add: 3/8 cup (needed) - 1/4 cup (have) = 3/8 - 2/8 = 1/8 cup
Answer: Since measuring 2/3 of an egg yolk is impractical, a better approach is to scale the recipe up to 3 whole egg yolks. To do this, add 1 whole egg yolk, 1/2 tablespoon of sugar, and 1/8 cup of white wine to what you already have.
Alternative (Simpler) Solution
Another way to approach the problem is to scale the recipe to an easy, whole-number multiple. You currently have 4 tbsp of sugar. The original recipe called for 3 tbsp, so a doubled recipe would call for 6 tbsp. This is an easy target to reach.
Step 1: Adjust sugar to double the recipe.
Add 2 tbsp of sugar to the 4 tbsp you already have to make 6 tbsp, which is exactly double the original amount.Step 2: Double all other ingredients for the total recipe.
Total Egg Yolks Needed: 2 yolks × 2 = 4 yolks
Total White Wine Needed: ¼ cup × 2 = ½ cup
Step 3: Calculate what you still need to add.
You already have 2 yolks and ¼ cup of wine in the bowl.Egg Yolks to Add: 4 (needed) – 2 (have) = 2 whole yolks
White Wine to Add: ½ cup (needed) – ¼ cup (have) = ¼ cup
Answer (Alternative): A simpler way to fix the recipe is to make a double batch. Add 2 tablespoons of sugar, 2 whole egg yolks, and ¼ cup of white wine to what is already in the bowl.
- The store is selling lemons at 2 for $1. Each yields about 2 tablespoons of juice. How much will it cost to buy enough lemons to make a 9-inch lemon pie requiring ½ cup of lemon juice?
Answer (click to Show/Hide)
To solve this, we will work backward from the amount of juice required to find the number of lemons needed, and then calculate the total cost.
Step 1: Convert the required juice from cups to tablespoons.
The recipe requires ½ cup of juice. We need to find the equivalent amount in tablespoons to match the yield per lemon. (Conversion: 1 cup = 16 tablespoons)Step 2: Determine how many lemons are needed.
We need 8 tablespoons of juice, and each lemon yields 2 tablespoons. We can set this up as a conversion to cancel the "tbsp" unit.Step 3: Calculate the cost of the lemons.
We need 4 lemons, and they are sold at a rate of 2 for $1. We set this up as a final conversion to find the total cost.Answer: It will cost $2 to buy enough lemons for the pie.
- A car is driving at 45 miles per hour. How far does it travel in 2 seconds? Round your answer to the nearest foot.
Answer (click to Show/Hide)
To solve this, we first need to convert the car's speed from miles per hour into feet per second. Then we can use the formula Distance = Rate × Time to find the distance traveled. (Conversions: 1 mile = 5280 feet, 1 hour = 60 minutes, 1 minute = 60 seconds)
Step 1: Convert the speed to feet per second.
We set up a series of multiplications to cancel out the unwanted units (miles, hours, minutes) and leave us with feet per second.Step 2: Calculate the distance traveled in 2 seconds.
Now we use the converted rate (66 ft/sec) and the given time (2 sec) in the formula Distance = Rate × Time.The result is a whole number, so no rounding is necessary.
Answer: The car travels 132 feet in 2 seconds.
- Convert 245 in2 to ft2. Round your answer if needed to nearest tenth place.
Answer (click to Show/Hide)
To solve this, we will treat the square units as a product. For example, 245 in^2 is the same as 245 in × in. To convert to ft^2, we must convert each "inch" unit to "feet" by applying the conversion factor (1 ft = 12 in) twice.
We set up the problem to cancel out each "in" unit individually.
After cancelling the units, we multiply the remaining numbers. This gives us ft × ft in the numerator, which is ft^2.
Rounding to the nearest tenth place gives us 1.7 ft^2.
Answer: 245 in^2 is approximately 1.7 ft^2.
- Convert 12,000 m2 to km2. Round your answer if needed to nearest hundredth place.
Answer (click to Show/Hide)
We will solve this by treating the square units as a product (m^2 = m × m). To convert to km2, we must convert each "meter" unit to "kilometers" by applying the conversion factor (1 km = 1000 m) twice.
First, we set up the problem to cancel out each "m" unit individually.
After cancelling the units, we are left with km × km in the numerator (which is km2) and the remaining numbers to multiply.
Rounding to the nearest hundredth place gives us 0.01 km2.
Answer: 12,000 m2 is approximately 0.01 km2.
- Convert 3 yd3 to ft3. Round your answer if needed to nearest tenth place.
Answer (click to Show/Hide)
We will solve this by treating the cubic units as a product (yd3 = yd × yd × yd). To convert to ft3, we must convert each "yard" unit to "feet" by applying the conversion factor (1 yd = 3 ft) three times.
First, we set up the problem to cancel out each "yd" unit individually.
After cancelling the units, we are left with ft × ft × ft in the numerator (which is ft3) and the remaining numbers to multiply.
No rounding is needed for this answer.
Answer: 3 yd3 is equal to 81 ft3.
- Find the perimeter and area of a rectangle with width 2 feet and length 35 inches.
Answer (click to Show/Hide)
First, we need to work with consistent units. We will convert the width from feet to inches, since the length is already in inches.
Step 1: Convert units.
We use the conversion factor 1 ft = 12 in.
Now we have a width of 24 inches and a length of 35 inches.Step 2: Calculate the Perimeter.
The formula for the perimeter of a rectangle is P = 2(length + width).
Step 3: Calculate the Area.
The formula for the area of a rectangle is A = length × width.
Answer: The perimeter is 118 inches (or 9 ft 10 in). The area is 840 in2 .
- Find the length of a rectangle with a perimeter of 80 inches and width of 25 inches.
Answer (click to Show/Hide)
We will use the formula for the perimeter of a rectangle, P = 2(L + W), where P is the perimeter, L is the length, and W is the width.
Step 1: Set up the equation.
Substitute the given values for the perimeter (P = 80 in) and width (W = 25 in) into the formula.
Step 2: Solve for the length (L).
First, divide both sides of the equation by 2.
Next, subtract 25 from both sides to isolate L.
Answer: The length of the rectangle is 15 inches.
- The area of a rectangular region is 221 ft2. If the length is 156 inches, then what is the perimeter?
Answer (click to Show/Hide)
To find the perimeter, we first need to find the width of the rectangle. Since the area is given in square feet and the length in inches, we must convert the units to be consistent. We will convert the length to feet.
Step 1: Convert the length from inches to feet.
We use the conversion factor 1 ft = 12 in.
The length of the rectangle is 13 feet.Step 2: Use the area formula to find the width.
The formula for the area of a rectangle is A = L × W. We know the area (A = 221 ft2 ) and the length (L = 13 ft).
To find the width (W), we divide the area by the length.
The width of the rectangle is 17 feet.Step 3: Calculate the perimeter.
The formula for the perimeter of a rectangle is P = 2(L + W).
Answer: The perimeter of the rectangular region is 60 feet.
- The area of a rectangular room is 168 square feet. The length is 4 yds. What is the width in yds?
Answer (click to Show/Hide)
The area is given in square feet, but the length and the desired unit for the width are in yards. First, we must convert the units to be consistent. We will convert the area from square feet to square yards.Step 1: Convert the area to square yards.
We use the conversion factor 1 yd = 3 ft. Since we are working with square units, we can treat yd2 as yd × yd. To convert ft2 to yd2, we must apply the conversion factor twice to cancel out both instances of ft.
The area of the room is 56/3 yd2.Step 2: Use the area formula to find the width.
The formula for the area of a rectangle is A = L × W. We know the area (A = 56/3 yd2) and the length (L = 4 yds).
To find the width (W), we divide the area by the length.
Answer: The width of the room is 14/3 yards, or approximately 4.67 yards.
- The area of a triangular window is 90 square meters. The base of the window is 15 yards. What is the window’s height in yards?
Answer (click to Show/Hide)
The area is given in square meters, but the base and the desired unit for the height are in yards. First, we must convert the units to be consistent. We will convert the area from square meters to square yards.
Step 1: Convert the area to square yards.
We use the conversion factor 1 yd ≈ 0.9144 m. Since we are working with square units, we can treat m2 as m × m. To convert m2 to yd2, we must apply the conversion factor twice.
The area of the window is approximately 107.64 yd2.Step 2: Use the area formula to find the height.
The formula for the area of a triangle is A = ½ × b × h. We know the area (A ≈ 107.64 yd2) and the base (b = 15 yds).
To find the height (h), we can first multiply the base by ½.
Now, we divide the area by the result.
Answer: The height of the window is approximately 14.35 yards.
- Jose just removed the children’s playset from his back yard to make room for a rectangular garden. He wants to put a fence around the garden to keep out the dog. He has a 50 foot roll of fence in his garage that he plans to use. To fit in the backyard, the width of the garden must be 10 feet. How long can he make the other side if he wants to use the entire roll of fence?
Answer (click to Show/Hide)
The total length of the fence represents the perimeter of the rectangular garden. We are given the perimeter and the width and need to find the length.
Step 1: Use the perimeter formula for a rectangle.
The formula for the perimeter (P) of a rectangle is P = 2L + 2W, where L is the length and W is the width. We know P = 50 ft and W = 10 ft.
Step 2: Simplify the equation.
First, calculate the value for the width component of the formula.
Step 3: Solve for the length (L).
Subtract 20 ft from both sides of the equation to isolate the term with L.
Now, divide by 2 to find the value of L.
Answer: He can make the other side 15 feet long.
- A childs sandbox needs to be filled with sand. The dimensions of the box are 4 ft by 4 ft and is 16 inches deep. Find the volume rounded to the nearest cubic ft.
Answer (click to Show/Hide)
To find the volume, all dimensions must be in the same unit. We will convert the depth from inches to feet before calculating the volume.
Step 1: Convert the depth to feet.
We use the conversion factor 1 ft = 12 in.
Step 2: Calculate the volume.
The formula for the volume (V) of a rectangular box is V = Length × Width × Height.
Step 3: Convert to a decimal and round.
The question asks to round the answer to the nearest cubic foot.
Rounding to the nearest whole number gives us 21 ft3.Answer: The volume of the sandbox is approximately 21 cubic feet.
- A box is created from a 6 ft by 4 ft piece of cardboard. To create the box a square piece is cut out from each corner. The square piece measures 2 in by 2 in. The sides are then folded up and taped together. Find the Volume of the box rounded to the nearest tenth of a cubic ft.
Answer (click to Show/Hide)
First, all dimensions must be in the same unit. Since the final answer is required in cubic feet, we will convert the dimensions of the cut-out square from inches to feet.
Step 1: Convert the cut-out dimension to feet.
The side length of the cut-out square determines the height of the box.
The height of the box will be 1/6 ft.Step 2: Determine the length and width of the box.
The length and width of the box are the original dimensions of the cardboard minus the length of the two cut-outs on each side.
Step 3: Calculate the volume.
The formula for the volume (V) is V = Length × Width × Height.
Step 4: Convert to a decimal and round.
The question asks to round the answer to the nearest tenth of a cubic foot.
Rounding to the nearest tenth gives us 3.5 ft3.Answer: The volume of the box is approximately 3.5 cubic feet.
- A circular pool needs to be repainted inside. The diameter of the pool is measured to be 14 ft and the depth is 5 ft and 8 inches. Find the surface area for the interior of the pool rounded to the nearest square ft (keep in mind the sides and bottom is the only region needing to be painted).
Answer (click to Show/Hide)
The total surface area to be painted is the sum of the area of the circular bottom and the lateral surface area (the side wall). First, all dimensions must be in the same unit.
Step 1: Convert the depth to feet.
The depth is given as 5 ft 8 in. We convert the inches to feet.
Total depth (h) =Step 2: Calculate the area of the circular bottom.
The formula for the area of a circle is A = πr2. The diameter is 14 ft, so the radius (r) is 7 ft.
Step 3: Calculate the lateral surface area of the side wall.
The side wall, if unrolled, is a rectangle. Its length is the circumference of the pool (C = 2πr), and its height is the depth of the pool.Step 4: Find the total surface area.
Add the area of the bottom and the area of the side.
Now, convert to a decimal and round to the nearest whole number.
Answer: The surface area to be painted is approximately 403 square feet.
- A local pool used by lap swimmers has dimensions 25 yd by 20 yd and is 5 feet deep. Find the cost for filling the pool if the city charges $1.50 per 1000 gallons. Use the conversion 1 gallon = 0.134 cubic ft.
Answer (click to Show/Hide)
To solve this, we must first find the volume of the pool in a consistent unit (cubic feet), then convert that volume to gallons, and finally calculate the total cost.
Step 1: Convert all dimensions to feet.
The length and width are given in yards. We will convert them to feet using the conversion 1 yd = 3 ft.
The depth is already 5 ft.Step 2: Calculate the volume in cubic feet.
The formula for the volume (V) of a rectangular prism is V = Length × Width × Depth.
Step 3: Convert the volume from cubic feet to gallons.
Using the given conversion, 1 gallon = 0.134 ft3.
Step 4: Calculate the total cost.
The city chargesAnswer: The cost to fill the pool is approximately $251.87.
Attributions
- This page contains modified content from David Lippman, "Math In Society, 2nd Edition." Licensed under CC BY-SA 4.0.
- This page contains modified content and images from "OpenStax PreAlgebra" by Lynn Marecek, MaryAnne Anthony-Smith. Licensed under CC BY-NC 4.0 / A derivative from the original work
- This page contains modified content and images from "Contemporary Mathematics" by Donna Kirk and is licensed under CC BY-NC 4.0 / A derivative from the original work.
- This page contains content by Robert Foth, Math Faculty, Pima Community College, 2021. Licensed under CC BY 4.0.
- Portions of the exercise solutions in this answer key were generated with the assistance of Gemini, a large language model from Google.