1.2 Percentages

1.2: Percentages
Learning Objectives
Upon completion of this section, you should be able to
- Convert between percent, decimal, and fractional values.
- Calculate the total, percent, or part.
- Solve application problems involving percentages.
- Calculate a flat tax.
- Calculate a progressive tax.
Percentages
In 2020, the U.S. federal government budgeted $3.5 billion for the National Park Service, which appears to be a very large number (and is!) and a large portion of the total federal budget. However, the total outlays from the U.S. federal government in 2020 was $6.6 trillion. So, the amount budgeted for the National Park Service was less than one-tenth of 1 percent, or 1/10%, of the total outlays. This percent describes a specific number by relating the size of a part to a whole. Understanding that ratio puts the $3.5 billion budgeted to the National Park Service in perspective.
After reviewing the fundamentals of percentages we will examine applications including calculating flat taxes, tips, discounts based on percentages for a purchase, and progressive income tax.
The word percent comes from the Latin phrase per centum, which means “by the hundred.” It is really two words, “per cent,” and means per one hundred. The percentage of something is a ratio that compares the relative size of a part to a whole.
Changing a percent to a fraction is to write the percent in its fractional form. To write n% in its fractional form is to write the percent as the fraction .
When we write 40%, this is equivalent to the fraction or the decimal 0.40. Notice that 80 out of 200 and 10 out of 25 are also 40%, since .
We will always do calculations with a percent after it has been converted to a decimal or fractional form. In the definition below when you see the equation the percent has been converted to a fractional or decimal form.
Percent
A percent represents a ratio or a fraction whose denominator is 100.
If we have a part that is some percent of a whole, then
or
Example 1
243 people out of 400 state that they like dogs. What percent is this?
Solution
The whole is the 400 and the part is the 243, so
Now if we move the decimal place over two to the right and divide by 100 we have an equivalent fraction and can then use the definition to write this as a percent.
This is now rewritten with the percent sign to be 60.75%.
If the value is written in a decimal or integer form, then the percent can be found from the equivalent decimal by moving the decimal point two places to the right. So, the value 0.6075 is rewritten with the percentage sign as 60.75% by moving the decimal place two places to the right.
Video Solution (1 min 42 secs – CC) Another example starts after the 1:42 mark of the video.
It is important that we convert a percent to a decimal or fractional form in many of the equations we use.
Converting between a Percent to Decimal or Fractional Form
Percent to Decimal: To write n% in its decimal first drop the % symbol and then divide n by 100.
Percent to Fraction: To write n% in its fractional form, crop the % symbol and write n over 100: . If possible simplify by writing fraction in lowest terms.
Decimal or Fraction to Percent: To convert the number x to percent, multiply x by 100 and place a percent sign, %, after the number, (x·100)%.
In this text we will mainly be using percentages that are written in a decimal form.
Example 2
Convert the percentage in the table below to decimal and fractional form.
| Percent | Decimal | Fraction |
|---|---|---|
| 6% | ||
| 78% | ||
| 135% | ||
| 12.5% |
Solution
Figure 1 shows how the given percents are converted to decimals by moving the decimal point two places to the left. Notice that we may need to add zeros in front of the number when moving the decimal to the left.
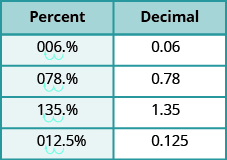
The table below shows the results from the conversions.
| Percent | Decimal |
|---|---|
| 6% | 0.06 |
| 78% | 0.78 |
| 135% | 1.35 |
| 12.5% | 0.125 |
To convert each of the percentages to fractional form we will divide each percent by 100 and remove the percent symbol.
| Percent | Decimal | Fraction |
|---|---|---|
| 6% | 0.06 | |
| 78% | 0.78 | |
| 135% | 1.35 | |
| 12.5% | 0.125 |
Example 3
Write each as a percent:
- 0.02
- 2.35
Solution
For each number we multiply by 100 and add the percent symbol %.
In the video below the presenter uses the approach of rewriting the number per 100 to find the percent. Both methods yield the same result.
Video Solution (3 mins 43 secs – CC) Another example starts after the 3:43 mark of the video.
Try it Now 1
Part 1
Convert the following to percent:
- 0.121
- 2.72
- 0.085
Part 2
Convert the percent to decimal:
- 5.65%
- 10.2%
- 0.65%
Hint 1 (click to Show/Hide)
Decimal or Fraction to Percent: To convert the number x to percent, multiply x by 100 and place a percent sign, %, after the number, (x·100)%.
Percent to Decimal: To write n% in its decimal form by dividing the n by 100 and representing the result as a decimal without the % symbol.
Answer (click to Show/Hide)
Part 1:
Part 2:
Calculate the total, percent, or part.
Now lets revisit that definition we gave on a percent and look at how we go between the percent, whole and part.
Percent
A percent represents a ratio or a fraction whose denominator is 100.
If we have a part that is some percent of a whole, then
or
Example 4
Find the percent of a whole
- Determine 70% of 3,500
- Determine 156% of 720
Solution
- The whole is 3,500 and the percent is 0.70 in decimal form. To find the part, or percent of the whole, substitute those values into the formula and calculate.
From this, we say that 70% of 3,500 is 2,450 - The whole is 720 and the percent is 1.56 in decimal form. To find the part, or percent of the whole, substitute those values into the formula and calculate.
From this, we say that 156% of 720 is 1,123.2.
Take a look at an example of how we use this definition to find the percent of some number (i.e. find the part related to a certain percent).
Example 5
What number is 35% of 90?
Solution
Translate this question into algebra. Let n be the number (part of the whole) and use that definition. We know the whole is 90 and the percent is 35%. Make sure to convert that percent to a number.
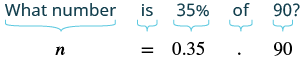
This gives us the following equation and solution:
We find that 31.5 is 35% of 90.
Example 6
36 is 75% of what number?
Solution
Translate this question into algebra. Let b be the number (the whole this time) and use the definition. We are given this time the part is 36 and the percent is 75%. Make sure to convert that percent to a number.
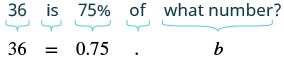
To solve that equation we need to divide both sides by 0.75:
We find that 36 is 75% of 48.
Try it Now 2
Answer the following:
- Determine 12.5% of 2,450.
- What is the whole if 10% of the whole is 4,000?
- What percent of 228 is 155?
Answer (click to Show/Hide)
-
- The whole is 2,450 and the decimal form of 12.5% is 0.125. To find the part, or percent of the whole, substitute those values into the formula and calculate.
From this, we say that 12.5% of 2,450 is 306.25. - Step 1: The percent is 10, which in decimal form is 0.1. We were given that 10% of the whole is 4,000, so the part is 4,000. Substituting into the formula, we have
Step 2: To find the whole, we solve the equation for the whole.From this we see that 40,000 is the whole, or that 10% of 40,000 is 4,000.
- Step 1: The whole is 228, the percent of the whole is 155. Substituting into the formula, we have
Step 2: To find the percent, we solve the equation for the percent.
- The whole is 2,450 and the decimal form of 12.5% is 0.125. To find the part, or percent of the whole, substitute those values into the formula and calculate.
We see the percent is 0.6798 (rounded to four decimal places). Converting from the decimal form yields 67.98%. We say that 155 is 67.98% of 228.
Solve Application Problems Involving Percents
Percents are frequently used in finance, purchases, taxes, research, science experiments, politics, and even casual conversation. Understanding these types of values helps when consuming media or discussing finances, for instance. Effectively working with and interpreting numbers and percents will help you become an informed consumer of this information.
In most cases, working through what is presented requires you to identify that you are indeed working with a question of percents, which two of the three values that are related through percents are known, and which of the three values you need to find.
Sales tax is something we all have to deal with when purchasing a product from a business (in most states in the U.S.). Although many states do collect sales tax the rate itself is composed of a state rate and local rate. We will only look at an overal sales tax rate in our applications to keep the discussion easier to follow. Even states without an official sales tax for consumers may have some sort of sales tax at a local level or at the business level.
Sales Tax and Total Price
Sales tax is a percent of the purchase price.
Or we can rewrite the Total Price as:
When the sales tax calculation results in a fraction of a penny, then normal rounding rules apply, round up for half a penny or more, but round down for less than half a penny.
Example 7
The sales tax in a town is 9.4%. How much tax will you pay on a $140 purchase?
Solution
Here, $140 is the whole, and we want to find 9.4% of $140. We start by writing the percent as a decimal by moving the decimal point two places to the left (which is equivalent to dividing by 100). We can then compute the tax:
The sales tax is $13.16 on a $140 purchase.
Video Solution (1 min 43 secs – CC)
Example 8
Cathy bought a bicycle in Tucson that had a purchase price of $392. Find the following:
- the sales tax paid where the overall sales tax rate was 8.7% of the purchase price.
- the total cost of the bicycle.
Solution
- Let t be the sales tax. The sales tax is 8.7% of the purchase price, so
. Which gives us that the sales tax is $34.10. - The total cost for the bicycle, c, is the original price plus the sales tax.
- The total cost is $426.10.
Tips work much like sales tax. They take a percent of the total bill and are typically calculated before the sales tax has been applied (pre-tax). You then add the tip and sales tax to the purchase price to find the total price.
Tips, Sales Tax, and Total Price
Example 9
A couple enjoyed a dinner at a restaurant. The bill for the dinner was $68.50 (before taxes). They want to leave an 18% tip based on the bill total. If the tip will be 18%, then how much is that tip?
Solution
We are asked to find the amount of the tip, so let t = amount of tip.
Write out what we are solving for and translate to an equation.
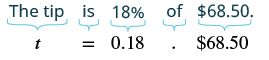
We found the tip was equal to $12.33. One thing you should plan on doing after finding a value is seeing if that number appears reasonable. Since $6.85 is 10% of the bill and if we double that we have $13.70 and would be 20% of the bill the value $12.33 seems reasonable as it is close to that 20% value of the bill.
We find that the couple should leave a tip of $12.33.
Example 10
A couple goes out to El Charro Café and orders drinks and food that adds up to $63.98. If the sales tax in Tucson is 8.7% and the couple wants to leave a tip of 18%, then what is the total price of the meal?
Solution
Step 1: Calculate the Sales Tax
Step 2: Calculate the Tip
Step 3: Find the Total Price
The couple would pay a total price of $81.07 for the meal.
As a side note. It is okay to switch the order of step 1 and 2 as both are only using the purchase price of the meal. Often you are given a total price for the meal that already includes the sales tax on the receipt, but you should see a purchase price pre sales tax as well.
Time to practice applying what you have seen on a bit more challenging problem. See how you do on the Try It Now problem below
Try it Now 3
A TV originally priced at $799 is on sale for 30% off. A sales tax of 9.2% is then applied. Find the price after including the discount and sales tax.
Hint 1 (click to Show/Hide)
You will have to compute the sales tax after you find the sale price. Start with finding the amount of the discount and removing that amount from the original price.
Hint 2 (click to Show/Hide)
The sale price is the original price minus the 30% discount. Find 30% of the original price and now subtract this amount from the original price.
The $239.70 is the amount we are subtracting from the original price of the TV.
The Sale price is .
Find the total now with the sales tax.
Hint 3 (click to Show/Hide)
Tax is added to the sale price. Determine the amount of sales tax to collect and add that to the sale price to find the total.
Answer (click to Show/Hide)
The sales price is first found by subtracting the discount of 30% from the original price:
The sales tax is:
After the discount and tax, the price is .
Percent Increase and Decrease Applications
The work we have done on applications with sales tax can lead us to a general strategy for finding the new amount after a percent increase or decrease.
We are often interested in the amount of an increase or decrease based on a percentage. To find the percent increase, first we find the amount of increase, which is the difference between the new amount and the original amount. Then we find what percent the amount of increase is of the original amount.
Finding the percent decrease is very similar to finding the percent increase, but now the amount of decrease is the difference between the original amount and the final amount. Then we find what percent the amount of decrease is of the original amount.
We can represent these calculations below.
Percent Increase and Decrease
Finding new amount after a percent increase or decrease.
Let p be the percent increase or decrease in a decimal format. When working with a percent decrease p will be a negative value. The new amount is found by:
Percent Increase and Percent Decrease Formulas
When we compute percent increase or decrease we always compare how much a quantity has changed to the original amount.
Example 11
In 2011, the California governor proposed raising community college fees from $26 per unit to $36 per unit. Find the percent increase. (Round to the nearest tenth of a percent.)
Solution
In this problem we are looking for the percent increase. Let p represent that increase. We can now solve for p using the percent increase formula.
The new fees represent approximately a 38.5% increase over the old fees.
Example 12
The value of a car dropped from $7400 to $6800 over the last year. What percent decrease is this? Round your answer to the nearest tenth of a percent.
Solution
In this problem we are looking for the percent decrease. Let p represent that percent decrease. We can now solve for p using the percent decrease formula.
We find that the value of the car dropped by approximately 8.1%.
Example 13
In the news, you hear “tuition is expected to increase by 7% next year.” If tuition this year was $1200 per quarter, what will it be next year?
Solution
In this scenario we do not know the new amount, a, after the increase.
We find that the new tuition for next year is going to be $1284.
Video Solution (1 min 44 secs – CC) Alternative method for solving is shown. Another example starts after the 1:44 mark on the video.
We can also use the formulas to solve questions about finding the original amount after a percent increase or decrease is observed.
Example 14
A store is advertising a sale where everything is 30% off. If the sale price is $22.40 on an item, then was was the original price?
Solution
In this scenario we are given the new value after a percent discount is taken. The original value is what we are trying to identify. Let n be the original amount, then we can find n by
We find that the original amount of the item was $32.
Check: If you take 30% of $32 and subtract it from that price you do get the sales price of $22.40 as a check on the work
In the example above it is far too tempting to take 30% of $22.40 and add that to the sales price to get the original amount. The problem is that if you try that approach you are not actually discounting the original price by 30% to get the sales price. Try it yourself and see what happens (you will get a different answer plus that answer you get if you discount it by 30% will not get you the sales price).
When the original value is not known, but the new amount and percent increase or decrease is given we can rewrite the original equations in a new form using a little algebra. Those new forms are given below.
Percent Increase and Percent Decrease Formulas (solved for original amount)
In these formulas put in percent decrease and percent increase in decimal form.
.
Try it Now 4
An advertisement shows a TV is on sale for $487.50. If that advertisement stated that it was 35% off,
then what was the original price?
Hint 1 (click to Show/Hide)
You are given a new amount and the percent decrease.
Answer (click to Show/Hide)
Let p be the original price of the TV. Use the formula for the original amount where a percent
decrease is applied:
We find the orignal price of the TV to be $750.
Flat and Progressive Taxes
In some states the amount of income tax calculated is done with a flat rate tax. A flat rate tax is one in which regardless of income everyone pays the same percent on that income. It does not mean that everyone pays the same amount in taxes. Sales tax is not considered to be a flat tax rate system as the proportion of your income going to sales tax goes up as your income decrease (we call sales tax a type of regressive tax system as it has a larger impact on those whose income is lower).
In 2021 the following states had a flat income tax rate system: Colorado, Illinois, Indiana, Kentucky, Massachusetts, Michigan, New Hampshire (interest and dividend income only). North Carolina, Pennsylvania, and Utah.
Example 15
A resident in Illinois has found that they have a taxable net income of $39,500 for line 11 on 2020 Form
IL-1040. Find the result for line 12.

Solution
The instructions for line 12 state to multiply line 11 by 4.95%. The value in line 11 was given to us as
$39,500, so we have line 12 as:
In most states the type of income tax paid is similar to the federal income tax rate where the tax rate changes to higher values as the taxable income amount increases. This type of tax system is referred to as a Graduated-rate or progressive income tax. In Arizona the state income tax is caclulate with a graduated-rate schedule.
Example 16
The 2020 Arizona graduated tax rate is given in the table below for those filing status is single or married filing separate. To use this table you will calculate the amount of money to be taxed at each level and then sum up the amount for each given tax rate. Find the income tax for a person filing single and has a taxable income reported as $60,000.
| Income | Tax Rate |
|---|---|
| The income between $0 and $27,272 | 2.59% |
| The income between $27,272 and $54,544 | 3.34% |
| The income between $54,544 and $163,632 | 4.17% |
| The income above $163,632 | 4.50% |
Solution
If the taxable income is $60,000 we will need to find the tax for each portion on the first three rows from the tax table given above. The first $27,272 is taxed at a rate of 2.59%. From row 2
is taxed at a rate of 3.34%. The amount above $54,544, which is
is taxed at the rate 4.17%.
To help keep track of how much tax is paid we will add a column that shows how much money is being taxed for each given rate as well as a column for the tax amount for that income.
| Income | Tax Rate | Amount to be taxed | Tax |
|---|---|---|---|
| The income between $0 and $27,272 | 2.59% | $27,272 | $706.34 |
| The income between $27,272 and $54,544 | 3.34% | $27,272 | $910.88 |
| The income between $54,544 and $163,632 | 4.17% | $5,456 | $227.52 |
| The income above $163,632 | 4.50% | $0 | $0.00 |
The total tax calculated is
Try it Now 5
Find the income tax for a person filing single in Arizona with a taxable income of $37,900. Use the table below to determine the income tax:
| Income | Tax Rate |
|---|---|
| The income between $0 and $27,272 | 2.59% |
| The income between $27,272 and $54,544 | 3.34% |
| The income between $54,544 and $163,632 | 4.17% |
| The income above $163,632 | 4.50% |
Hint 1 (click to Show/Hide)
You will need to find the amount to be taxed at each level, so contruct a similar table as shown in the
previous example that has the amount to be taxed.
Answer (click to Show/Hide)
In the table we have the amount to be taxed at each rate as well as the tax amount.
| Income | Tax Rate | Amount to be taxed | Tax |
|---|---|---|---|
| The income between $0 and $27,272 | 2.59% | $27,272 | $706.34 |
| The income between $27,272 and $54,544 | 3.34% | $10,628 | $354.98 |
| The income between $54,544 and $163,632 | 4.17% | $0 | $0.00 |
| The income above $163,632 | 4.50% | $0 | $0.00 |
The total tax paid is
Exercises
- Convert each number to a percentage
- 0.731
- 0.0025
- 2.94
- 0.057
Answer (click to Show/Hide)
- 73.1%
- 0.25%
- 294%
- 5.7%
- 26%
- What number is 18% of 75?
Answer (click to Show/Hide)
Convert 18% to decimal:
Multiply:
- What number is 110% of 50?
Answer (click to Show/Hide)
Convert 110% to decimal:
Multiply:
- 30 is 75% of what number?
Answer (click to Show/Hide)
Let be the number we’re looking for
Write the equation:
Solve for :
- 10 is 15% of what number?
Answer (click to Show/Hide)
Let be the number we’re looking for
Write the equation:
Solve for :
- The sales tax is 8.7%. How much is the sales tax on a purchase of $250? What is the total cost of the purchase including sales tax?
Answer (click to Show/Hide)
First calculate the tax amount:
Next calculate the total cost:
- The sales tax is 6.2%. How much is the sales tax on a purchase of $95? What is the total cost of the purchase including sales tax?
Answer (click to Show/Hide)
First calculate the tax amount:Next calculate the total cost:
- A restaurant bill for a family of four is $75 before taxes and tip. If the sales tax is 8.7% and they wish to leave a tip of 18% on the original bill before taxes, then what is the total cost for the meal.
Answer (click to Show/Hide)
First calculate the tax amount:
Next calculate the tip amount (18% of original bill):
Lastly find the total of the bill with tax and tip:
- You receive a bill for a meal at a restaurant for $45.90, but it only lists the total after tax. How much was the original amount of the meal before taxes if the sales tax rate is 5.1%?
Answer (click to Show/Hide)
Let be the original amount
Write the equation to represent the unknown original amount increased by 5.1% tax to give the bill total of $45.90:
Now simplify the equation:
Solve for :
- You receive a bill for a meal at a restaurant for $89.24, but it only lists the total after tax. How much was the original amount of the meal before taxes if the sales tax rate is 8.7%?
Answer (click to Show/Hide)
First, define a variable for the unknown original amount of the meal. Let’s call it .
The total bill is the sum of the original meal cost () and the sales tax. The sales tax is 8.7% of the original amount, which can be written as . This gives us the equation:
Combine the terms with :
To solve for , divide both sides of the equation by 1.087:
Calculate the value and round to two decimal places for currency:
Answer: The original amount of the meal before tax was $82.10.
- Out of 230 racers who started the marathon, 212 completed the race, 14 gave up, and 4 were disqualified. What percentage did not complete the marathon? If you are disqualified from a race you can not be considered a completer.
Answer (click to Show/Hide)
First, find the total number of racers who did not complete the marathon. This includes those who gave up and those who were disqualified.
Next, calculate the fraction of racers who did not complete. This is the number of non-completers divided by the total number of racers who started.
To express this fraction as a percentage, multiply the fraction by 100.
Calculate the final value and round to two decimal places.
Answer: Approximately 7.83% of the racers did not complete the marathon.
- Patrick left an $8 tip on a $50 restaurant bill. What percent tip is that?
Answer (click to Show/Hide)
To find the tip percentage, you need to determine what part of the total bill the tip represents. This can be set up as a fraction.
To convert this fraction into a percentage, multiply it by 100.
Calculate the final value.
Answer: Patrick left a 16% tip.
- Ireland has a 23% VAT (value-added tax, similar to a sales tax). How much will the VAT be on a purchase of a €250 (250 Euros) item?
Answer (click to Show/Hide)
To calculate the VAT amount, you multiply the original price of the item by the VAT rate. First, convert the percentage to a decimal.
Now, set up the equation to find the VAT.
Calculate the final value.
Answer: The VAT on the item will be €57.50.
- Employees in 2012 paid 4.2% of their gross wages towards social security (FICA tax), while employers paid another 6.2%. How much would someone earning $45,000 a year have paid towards social security out of their gross wages in 2012?
Answer (click to Show/Hide)
The problem asks for the amount the employee paid, so we only need to use the employee’s tax rate of 4.2%. The employer’s rate is extra information. First, convert the employee’s percentage to a decimal.
Now, set up the equation to find the tax paid.
Calculate the final value.
Answer: The employee would have paid $1,890 towards social security in 2012.
- A project on Kickstarter.com was aiming to raise $15,000 for a precision coffee press. They ended up with 714 supporters, raising 557% of their goal. How much did they raise?
Answer (click to Show/Hide)
The problem asks for the total amount of money raised. The number of supporters is extra information. We need to calculate 557% of the $15,000 goal. First, convert the percentage to a decimal.
Now, set up the equation to find the total amount raised.
Calculate the final value.
Answer: They raised $83,550.
- Another project on Kickstarter for an iPad stylus raised 1,253% of their goal, raising a total of $313,490 from 7,511 supporters. What was their original goal? Round your answer to nearest thousand dollars.
Answer (click to Show/Hide)
Let the original goal be represented by the variable . The number of supporters is extra information that is not needed to solve for the goal.
The amount raised is the original goal multiplied by the percentage. First, convert the percentage raised into a decimal.
Set up the equation using the information from the problem.
To solve for , divide the total amount raised by the decimal percentage.
Calculate the final value.
Answer: The original goal was $25,000.
- A company wants to decrease their energy use by 15%.
- If their electric bill is currently $2,200 a month, what will their bill be if they’re successful?
- If their next bill is $1,700 a month, were they successful? Why or why not?
Answer (click to Show/Hide)
First, calculate the target bill amount for a 15% decrease. The decrease is 15% of the original amount. Convert the percentage to a decimal.
Calculate the monetary value of the decrease.
Subtract the decrease from the original bill to find the new target bill.
The second part of the problem asks if a new bill of $1,700 represents success. To be successful, the new bill must be less than or equal to the target bill.
Answer: Their target bill to achieve a 15% reduction is $1,870. They were successful, because their new bill of $1,700 is lower than their target bill of $1,870.
- A store is hoping an advertising campaign will increase their number of customers by 30%. They currently have about 80 customers a day.
- How many customers will they have if their campaign is successful?
- If they increase to 120 customers a day, were they successful? Why or why not?
Answer (click to Show/Hide)
First, calculate the target number of customers for a 30% increase. The increase is 30% of the original number of customers. Convert the percentage to a decimal.
Calculate the value of the increase in customers.
Add the increase to the original number of customers to find the new target.
The second part of the problem asks if an increase to 120 customers represents success. To be successful, the new number of customers must be greater than or equal to the target.
Answer: Their target is 104 customers a day to achieve a 30% increase. They were successful, because their new daily customer count of 120 is higher than their target of 104.
- An article reports “attendance dropped 6% this year, to 300.” What was the attendance before the drop?
Answer (click to Show/Hide)
Let the original attendance be represented by the variable . The new attendance is the result of a 6% drop from this original number.
A 6% drop means that 94% of the original attendance remains (100% – 6% = 94%). Convert this remaining percentage to a decimal.
Set up the equation. The original attendance multiplied by the remaining percentage equals the new attendance.
To solve for , divide the new attendance by the decimal percentage.
Calculate the value and round to the nearest whole number, since attendance involves people.
Answer: The attendance before the drop was approximately 319.
- An article reports “sales have grown by 30% this year, to $200 million.” What were sales before the growth?
Answer (click to Show/Hide)
Let the original sales be represented by the variable . The new sales figure is the result of a 30% growth from this original amount.
A 30% growth means that the new sales are 130% of the original sales (100% + 30% = 130%). Convert this total percentage to a decimal.
Set up the equation. The original sales multiplied by the new percentage equals the new sales figure.
To solve for , divide the new sales figure by the decimal percentage.
Calculate the value and round to the nearest dollar.
Answer: The sales before the growth were approximately $153,846,154.
- A store has clearance items that have been marked down by 60%. They are having a sale, advertising an additional 30% off clearance items. What percent of the original price do you end up paying?
Answer (click to Show/Hide)
Let the original price of the item be represented by the variable . The first markdown is 60%. This means you pay 40% of the original price.
The price after the first markdown (the clearance price) is 40% of the original price, .
The second discount is an additional 30% off the clearance price. This means you pay 70% of the clearance price.
Calculate the final price by taking 70% of the clearance price.
Multiply the decimals to find the final percentage of the original price.
This means the final price is , or 28% of the original price.
Answer: You end up paying 28% of the original price.
- Which is better: having a stock that goes up 30% on Monday then drops 30% on Tuesday, or a stock that drops 30% on Monday and goes up 30% on Tuesday? In each case, what is the net percent gain or loss?
Answer (click to Show/Hide)
Let the original price of the stock be represented by the variable . We will analyze both scenarios.
Scenario 1: Up 30% on Monday, then down 30% on Tuesday
- On Monday, the price increases by 30%. The new price is 130% of the original.
- On Tuesday, this new price drops by 30%. This means the final price is 70% of Monday’s price.
- Multiply the decimals to find the final percentage of the original price.
- The final price is 91% of the original price, which represents a 9% loss.
Scenario 2: Down 30% on Monday, then up 30% on Tuesday
- On Monday, the price drops by 30%. The new price is 70% of the original.
- On Tuesday, this new price increases by 30%. The final price is 130% of Monday’s price.
- Multiply the decimals to find the final percentage of the original price.
- The final price is also 91% of the original price, which represents a 9% loss.
Answer: Neither is better as you end up with the same loss of 9%.
- On Monday, the price increases by 30%. The new price is 130% of the original.
- The Inconsistent Books store changes the normal prices of books on Mondays and Tuesdays. On Monday the price of a book is 10% above the normal price. On Tuesday the price is 10% below the normal price. Sarah bought a book on Monday for $16.50. What would be the price of that book on a Tuesday?
Answer (click to Show/Hide)
First, determine the book’s normal price based on the Monday price. Let the normal price be . The Monday price is 10% above normal, or 110% of the normal price, which is $16.50.
Solve for the normal price by dividing the Monday price by 1.10. The normal price is $15.00.
Now, calculate the Tuesday price. The Tuesday price is 10% below the normal price, which means it is 90% of the normal price.
Calculate the final price.
Answer: The price of the book on a Tuesday would be $13.50.
- Determine the amount of taxes paid if you are a resident in Illinois with a calculated taxable net income of $102,500.

Answer (click to Show/Hide)
Identify the net income and the tax rate.
Net Income = $102,500
Tax Rate = 4.95%Convert the tax rate from a percentage to a decimal by dividing by 100.
Multiply the net income by the decimal tax rate to find the total tax paid.
Answer: The amount of taxes paid would be $5,073.75.
- If you were a resident of Illinois and your reported taxable net income doubled from $102,500 to $205,000 would your amount of taxes owe double on line 12?
Answer (click to Show/Hide)
First, calculate the tax on the original income of $102,500 with the flat tax rate of 4.95% (or 0.0495).
Next, calculate the tax on the doubled income of $205,000 using the same tax rate.
Compare the two tax amounts by dividing the new tax amount by the original tax amount.
Answer: Yes, the amount of taxes owed would double. The new tax amount ($10,147.50) is exactly twice the original tax amount ($5,073.75). This happens because Illinois uses a flat tax rate. Since the tax rate is a constant percentage, any change in income results in a directly proportional change in the tax owed.
- Answer the following about a resident filing single in Arizona for their income taxes in 2020. Use the table provided in example 16 to answer this question.
- Find the income tax for a person with a taxable income of $50,000.
- Find the income tax for a person with a taxable income of $20,000.
- Would the income tax for a person in Arizona double if their taxable income doubled?
- If a person had a taxable income of $30,000 would the income tax double if we double the taxable income to $60,000. Why or why not?
Answer (click to Show/Hide)
-
Find the income tax for a person with a taxable income of $50,000.
This requires a marginal tax calculation.
The first $27,272 is taxed at 2.59%.
The rest of the income ($50,000 – $27,272 = $22,728) is taxed at 3.34%.
The total tax would be $1,465.59. -
Find the income tax for a person with a taxable income of $20,000.
A taxable income of $20,000 falls entirely within the first bracket, so it is all taxed at 2.59%.
The tax would be $518. -
Would the income tax for a person in Arizona double if their taxable income doubled?
No. Because of the marginal tax brackets, as income increases, a larger portion of it is taxed at a higher rate. This means the total tax will increase by more than double if the income doubles and crosses into a new tax bracket. -
If a person had a taxable income of $30,000, would the income tax double if the taxable income was doubled to $60,000? Why or why not?
First, calculate the tax for each income level using a marginal tax table.
Tax on $30,000:Income Segment Amount Rate Tax $0 – $27,272 $27,272 2.59% $706.34 $27,272 – $30,000 $2,728 3.34% $91.12 Total $30,000 $797.46 Tax on $60,000:
Income Segment Amount Rate Tax $0 – $27,272 $27,272 2.59% $706.34 $27,272 – $54,544 $27,272 3.34% $910.88 $54,544 – $60,000 $5,456 4.17% $227.50 Total $60,000 $1,844.72 To check if the tax doubled, multiply the first tax amount by 2:
Since $1,844.72 is not equal to $1,594.92, the tax did not double. The tax on $30,000 is $797.46, while the tax on $60,000 is $1,844.72. The tax more than doubled because doubling the income pushed a portion of that income into a higher tax bracket (4.17%), leading to a higher overall effective tax rate.
Attributions
- This page contains modified content from David Lippman, “Math In Society, 2nd Edition.” Licensed under CC BY-SA 4.0.
- This page contains modified content and images from “OpenStax PreAlgebra” by Lynn Marecek, MaryAnne Anthony-Smith. Licensed under CC BY-NC 4.0 / A derivative from the original work
- This page contains modified content and images from “Contemporary Mathematics” by Donna Kirk and is licensed under CC BY-NC 4.0 / A derivative from
the original work. - This page contains content by Robert Foth, Math Faculty, Pima Community College, 2021. Licensed under CC BY 4.0.
- Portions of the exercise solutions in this answer key were generated with the assistance of Gemini, a large language model from Google.

