4.3 Measures of Central Tendency

Robert Foth

4.3 Measures of Central Tendency

4.3: Measures of Central Tendency

Learning Objectives

Upon completion of this section, you should be able to

Calculate the Mean, Median, and Mode for quantitative data

Calculating the Mean

It is often desirable to use a few numbers to summarize the distribution of the data you are working with. One important aspect of that distribution is where a center is located. Measures of central tendency are discussed first in this section. A second aspect of a distribution is how spread out it is. In other words, how much the data in the distribution vary from one another. The next section describes measures of variability. Both of these combined are typically how we describe data distributions numerically.

There are three main measures of central tendency that you’ll encounter in your studies:

Mean
Median
Mode

Each of these measures provides a different perspective on what constitutes the “center” of a dataset, and each has its own strengths and weaknesses depending on the nature of your data.

Mean: Often referred to as the “average,” the mean is calculated by summing all values in a dataset and dividing by the number of values. It’s sensitive to all values in the dataset, including outliers.
Median: This is the middle value when your data is arranged in order. It’s particularly useful when dealing with skewed distributions or datasets with extreme outliers.
Mode: The mode is simply the value that appears most frequently in your dataset. It’s the only measure of central tendency that can be used with nominal (categorical) data.

The first measure of center we will examine is the mean.

Mean

The mean for a set of quantitative data is the sum of the data values divided by the number of values.

If the data is from a sample we call it a sample mean and denote it with the letter x and a bar on top, $\bar{x}$ . For a sample we use a lower case n to represent the number of data values.

$\bar{x} = \frac{sum of all data values}{number of data values} = \frac{\sum x}{n} = \frac{x_{1} + x_{2} + \dots + x_{n}}{n}$

If the data is from a population we call it a population mean we denote it with the lowercase greek letter mu, μ (mew). For a population we typically use a capital N for the number of data values.

$μ = \frac{sum of all data values}{number of data values} = \frac{\sum x}{N} = \frac{x_{1} + x_{2} + \dots + x_{N}}{N}$

Why do we call it the mean and not average? We need to be careful with the word “average” as it means different things to different people in different contexts. One of the most common uses of the word “average” is what mathematicians and statisticians call the arithmetic mean, or just plain old mean for short. “Arithmetic mean” sounds rather fancy, but you have likely calculated a mean many times without realizing it; the mean is what most people think of when they use the word “average”.

Example 1

Marci’s exam scores for her last math class were: 79, 86, 82, 94. Find her mean exam score.

Solution

The mean of these values would be:

$\frac{79 + 86 + 82 + 94}{4} = 85.25$

Typically we round means to one more decimal place than the original data had. In this case, we would round 85.25 to 85.3.

Video Solution Example 1 (1 min 3 secs – CC) Another example starts after the 1:03 mark of the video.

Example 2

The number of touchdown (TD) passes thrown by each of the 31 teams in the National Football League in the 2000 season are shown below. Find the mean number of passes thrown.

37	33	33	32	29	28	28	23	22	22	22	21	21	21	20	20
19	19	18	18	18	18	16	15	14	14	14	12	12	9	6

Solution

Adding these values, we get 634 total TDs. Dividing by 31, the number of data values, we get 634/31 = 20.4516. It would be appropriate to round this to 20.5.

It would be most correct for us to report that “The mean number of touchdown passes thrown in the NFL in the 2000 season was 20.5 passes,” but it is not uncommon to see the more casual word “average” used in place of “mean.”

Video Solution Example 2 (2 mins 28 secs – CC)

Try it Now 1

The price of a jar of peanut butter at 5 stores was: $3.29, $3.59, $3.79, $3.75, and $3.99. Find the mean price.

Hint 1 (click to Show/Hide)

The mean is the arithmetic average of all data values (including repetitions of a data value). Use the definition to help guide you.

The mean of a set of data is the sum of the data values divided by the number of values.

$\bar{x} = \frac{sum of all data values}{number of data values} = \frac{\sum_{i = 1}^{n} x_{i}}{n} = \frac{x_{1} + x_{2} + \dots + x_{n}}{n}$

Answer (click to Show/Hide)

Adding the prices and dividing by 5 we get the mean price: $3.68 (rounded to nearest penny since we are dealing with money)

$\frac{3.29 + 3.59 + 3.79 + 3.75 + 3.99}{5} = 3.682$

Sometimes the data is given to us in a frequency table instead of a direct list of all values. When this happens we can still find the mean by recalling that repeated addition is actually just multiplication. So if we see the data value of 15 and has a frequency of 6 from the table we would in the formula for the mean add 15 six different times in the numerator. This would be the same as taking the value 15 and multiply by 6 (as we will see in the next example): $15 + 15 + 15 + 15 + 15 + 15 = 6 \cdot 15$

Example 3

The one hundred families in a particular neighborhood are asked their annual household income, to the nearest $5 thousand dollars. The results are summarized in a frequency table below. Find the mean household income.

Income (thousands of dollars)	Frequency
15	6
20	8
25	11
30	17
35	19
40	20
45	12
50	7

Solution

Calculating the mean by hand could get tricky if we try to type in all 100 values:

$\frac{\overset{6 terms}{\overset{︷}{15 + \dots + 15}} + \overset{8 terms}{\overset{︷}{20 + \dots + 20}} + \overset{11 terms}{\overset{︷}{25 + \dots + 25}} + \dots}{100}$

We could calculate this more easily by noticing that adding 15 to itself six times is the same as 15·6 = 90. Using this simplification, we get

$\frac{15 \cdot 6 + 20 \cdot 8 + 25 \cdot 11 + 30 \cdot 17 + 35 \cdot 19 + 40 \cdot 20 + 45 \cdot 12 + 50 \cdot 7}{100} = \frac{3390}{100} = 33.9$

The mean household income of our sample is 33.9 thousand dollars ($33,900).

Video Solution Example 3 (2 mins 34 secs – CC) Another example starts after the 2:34 mark of the video.

Example 4

Extending off the last example, suppose a new family moves into the neighborhood example that has a household income of $5 million ($5000 thousand). What is the mean household income?

Solution

Adding this to our sample, our mean is now:

$\frac{15 \cdot 6 + 20 \cdot 8 + 25 \cdot 11 + 30 \cdot 17 + 35 \cdot 19 + 40 \cdot 20 + 45 \cdot 12 + 50 \cdot 7 + 5000 \cdot 1}{101} = \frac{8390}{101} = 83.069$

While 83.1 thousand dollars ($83,069) is the correct mean household income, it no longer represents a “typical” value as it is larger than all but one value.

Video Solution Example 4 (1 mins 52 secs – CC)

Calculating the Median

Imagine the data values on a see-saw or balance scale. The mean is the value that keeps the data in balance, like in the picture below.

Balancing weights on a bar shows that a lot of weght on the left side shifts the location of the mean awawy from the middle of the beam and towards the left.

If we graph our household data, the $5 million data value is so far out to the right that the mean has to adjust up to keep things in balance

For this reason, when working with data that have outliers – values far outside the primary grouping – it is common to use a different measure of center, the median.

Median

The median of a set of data is the value in the middle when the data is in order from least to greatest.

To find the median:

Order the data from least to greatest.
Count the number of values (n).

If n is odd:

The median is the middle value.
The position of the median is: Find $\frac{n}{2}$ and round up to the next whole number.

If n is even:

The median is the average of the two middle values.
The middle values are: $\frac{n}{2} and \frac{n}{2} + 1$ .

Example (odd): In a dataset of 9 exam scores, the median is the 5th score.

Example (even): In a dataset of 10 exam scores, the median is the average of the 5th and 6th scores.

Example 5

Find the median of these quiz scores: 5 10 8 6 4 8 2 5 7 7

Solution

We start by listing the data in order: 2 4 5 5 6 7 7 8 8 10

Since there are 10 data values, an even number, there is no one middle number. So we find the mean of the two middle numbers.

The positions are: $\frac{10}{2} = 5 and \frac{10}{2} + 1 = 6$

Going through the data we see 6 is located in the 5th position and 7 is located in the 6th position. Take the mean of those two data values to get the median: $\frac{6 + 7}{2} = 6.5$

The median quiz score was 6.5.

Video Solution Example 5 (4 mins 43 secs – CC) Another example starts after the 3:45 mark of the video.

Example 6

The number of touchdown (TD) passes thrown by each of the 31 teams in the National Football League in the 2000 season are shown below. Find the median number of passes thrown.

37	33	33	32	29	28	28	23	22	22	22	21	21	21	20	20
19	19	18	18	18	18	16	15	14	14	14	12	12	9	6

Solution

Normally we would start by listing the data in order. Luckily, it was already in decreasing order, so we can work with it without needing to reorder it first.

Since there are 31 data values, an odd number, the median will be the middle value in the ordered lists. This position is found by taking $\frac{31}{2} = 15.5$ , and rounding up to 16. The value 16 is the position of the median, so we go back to the data and find that the 16th data value is 20. The median number of touchdown passes in the 2000 season was 20 passes. Notice that for this data, the median is fairly close to the mean we calculated earlier, 20.5.

Video Solution Example 6 (57 secs – CC)

Example 7

The following are the closing prices of 10 recent homes sold in a local market.

$229,000	$155,000	$109,000	$187,000	$182,000
$659,000	$215,000	$138,000	$174,000	$118,000

Find the median home sale price.

Solution

Organize the sales prices from smallest to largest and follow the rule for even number of data values as stated above.

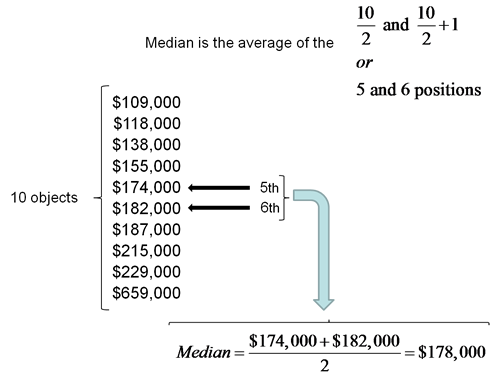
Sale prices listed smallest to largest pointing out the 5th and 6th term and averaging the result ($174,000 and $182,000) to get $178,000 for the Median

Try it Now 2

The price of a jar of peanut butter at 5 stores were: $3.29, $3.59, $3.79, $3.75, and $3.99. Find the median price.

Hint 1 (click to Show/Hide)

To find the median, begin by listing the data in order from smallest to largest, or largest to smallest.

If the number of data values, n, is odd, then the median is the middle data value. The position for the value can be found by rounding n/2 up to the next whole number.

If the number of data values is even, there is no one middle value, so we find the mean of the two middle values (the positions are at n/2 and n/2 + 1)

Answer (click to Show/Hide)

First we put the data in order: $3.29, $3.59, $3.75, $3.79, $3.99. Since there are an odd number of data, the median will be the middle value, $3.75.

If the data is provided in a frequency table we can still find the median, but we will need to use the frequency values to help locate positions of the data. The next example goes through the process of finding the median for that frequency table data.

Example 8

Let us return now to our original household income data from earlier. The one hundred families in a particular neighborhood are asked their annual household income, to the nearest $5 thousand dollars. The results are summarized in a frequency table below. Find the median household income.

Income (thousands of dollars)	Frequency
15	6
20	8
25	11
30	17
35	19
40	20
45	12
50	7

Solution

Here we have 100 data values. If we didn’t already know that, we could find it by adding the frequencies. Since 100 is an even number, we need to find the mean of the middle two data values – the 50th and 51st data values. To find these, we start counting up from the bottom:

There are 6 data values of $15, so Values 1 to 6 are $15 thousand
The next 8 data values are $20, so Values 7 to (6+8)=14 are $20 thousand
The next 11 data values are $25, so Values 15 to (14+11)=25 are $25 thousand
The next 17 data values are $30, so Values 26 to (25+17)=42 are $30 thousand
The next 19 data values are $35, so Values 43 to (42+19)=61 are $35 thousand

From this we can tell that values 50 and 51 will be $35 thousand, and the mean of these two values is $35 thousand. The median income in this neighborhood is $35 thousand.

Video Solution Example 8 (3 mins 27 secs – CC) Another example starts after the 2:15 mark of the video.

Example 9

Add in a new neighbor to our previous examples whose household income is $5 million. Find the new median.

Solution

If we add in the new neighbor with a $5 million household income, then there will be 101 data values, and the 51st value will be the median. As we discovered in the last example, the 51st value is $35 thousand. Notice that the new neighbor did not affect the median in this case. The median is not swayed as much by outliers as the mean is.

Video Solution Example 9 (1 mins 11 secs – CC)

Median vs Mean

Since the median is simply a location marker in the data set it is very resistant to extreme measurements in the data set.

–For instance if we use the median to measure the center of house prices in a local market the median will have very little change in value when a mansion is sold in that market as we can see from Example 7 if we compare the Median price of $178,000 to the Mean price of $216,600 (verify this calculation on your own).

When anybody gives you the “average” value for a data set you will want to make sure what you are dealing with as both the mean and median give a measure of the center of the data. There are times when the median is reported as an average or typical value instead of the mean. The home sales data can be used in two different ways depending on your perspective (a buyer or seller of a home).

The mean home prices are at $216,600. Wouldn’t it be a great time to sell! Call Sellme at 555-5550.

Thinking of moving to Tucson, give me a call the median home sales is currently at $178,000. Call BuyMeCheap at 555-5551.

Which measure of center you use can change the story about the data slightly. How do you know which one to pick? In most cases the mean will be a good choice, but not if there are extreme outliers or the data distribution is heavily skewed on one side. A safer assumption would be to use the mean with the data shows a symmetric distribution. We will not be going into how to measure skewness in this book, but it is a subject that has extensive literature in statistics (not a typical topic you will find in an introductory statistics course you may take in the near future).

Try it Now 3

The playbill for the Alley Theatre in Houston wants to appeal to advertisers. They reported the mean household income and the median age of theater goers.

What do you think?

What might have guided their choice of the mean or median?

Answer (click to Show/Hide)

It is likely that they wanted to emphasize that theater goers had high income but de-emphasize how old they are. The distributions of income and age of theater goers probably have positive skew. Therefore the mean is probably higher than the median. This results in higher income and lower age than if the median household income and mean age had been presented.

Mode

In addition to the mean and the median, there is one other common measurement of the “typical” value of a data set: the mode.

Mode

The mode is the element of the data set that occurs most frequently.

The mode is fairly useless with data like weights or heights where there are a large number of possible values. The mode is most commonly used for categorical (qualitative) data, for which median and mean cannot be computed.

Example 10

In our vehicle color survey, we collected the data below. Find the mode.

Car Color
Color	Frequency
Blue	25
Green	52
Red	41
White	36
Black	39
Grey	23

Solution

For this data, Green is the mode, since it is the data value that occurred the most frequently.

Video Solution Example 10 (48 secs – CC)

It is possible for a data set to have more than one mode if several categories have the same frequency, or no modes if each every category occurs only once or the same amount.

Try it Now 4

Reviewers were asked to rate a product on a scale of 1 to 5. Find

The mean rating
The median rating
The mode rating

Product Rating Scores
Rating	Frequency
1	5
2	7
3	7
4	3
5	1

Answer (click to Show/Hide)

The mean is $\frac{1 \cdot 5 + 2 \cdot 7 + 3 \cdot 7 + 4 \cdot 3 + 5 \cdot 1}{23} \approx 2.5$

There are 23 data values, so the median will be the 12th data value. Ratings of 1 are the first 5 values, while a rating of 2 are the next 7 values, so the 12th value will be a rating of 2. The median is 2.

The mode is the most frequent rating. The largest frequency is 7, but in this case there are two ratings (2 and 3) with that frequency. The mode is the rating 2 and 3.

Exercises

The table below shows scores on a Math test. Compute the Mean, Median, and Mode. Round your answer to two places.

80 50 50 90 70 70 100 60 70 80 70 50

90 10 80 70 30 80 80 70 100 60 60 50
Answer (click to Show/Hide)
1. Mean is 67.5
2. There are 24 data values. Order the data and the median is located at the mean of the
  $\frac{24}{2} = 12 and \frac{24}{2} + 1 = 13$ positions. The median is
  $\frac{70 + 70}{2} = 70$
3. The data value 70 is repeated the most (six times) and is the mode.
A group of adults where asked how many cars they had in their household. Compute the Mean, Median, and Mode. Round your answer to two places.

1 4 2 2 1 2 3 3 1 4 2 2

1 2 1 3 2 2 1 2 1 1 1 2
Answer (click to Show/Hide)
1. Mean is 1.92
2. There are 24 data values. Order the data and the median is located at the mean of the $\frac{24}{2} = 12 and \frac{24}{2} + 1 = 13$ positions.
  The median is $\frac{2 + 2}{2} = 2$
3. The data value 2 is repeated the most (six times) and is the mode.
A group of diners were asked how much they would pay for a meal. Their responses were: $7.50, $8.25, $9.00, $8.00, $7.25, $7.50, $8.00, $7.00.
1. Find the mean
2. Find the median
Answer (click to Show/Hide)
1. Mean: $\frac{7.5 + 8.25 + 9 + 8 + 7.25 + 7.5 + 8 + 7}{8} = 7.8125$ or approximately $7.82
2. Median: There are 8 values, so the median is found by taking the mean of the $\frac{8}{2} = 4 and \frac{8}{2} + 1 = 5$ positions.
  The median is $\frac{7.5 + 8.0}{2} = 7.75$
You recorded the time in seconds it took for 8 participants to solve a puzzle. The times were: 15.2, 18.8, 19.3, 19.7, 20.2, 21.8, 22.1, 29.4.
1. Find the mean to two decimal places
2. Find the median
Answer (click to Show/Hide)
1. Mean: $\frac{15.2 + 18.8 + 19.3 + 19.7 + 20.2 + 21.8 + 22.1 + 29.4}{8} = 20.8125$ or approximately 20.81 seconds.
2. Median: There are 8 values, so the median is found by taking the mean of the $\frac{8}{2} = 4 and \frac{8}{2} + 1 = 5$ positions.
  The median is $\frac{19.7 + 20.2}{2} = 19.95$
Jasmine collected data on how many days it would take an order from Netflix to arrive at her door. Find the mean, median and mode for the number of days for the order to arrive at her door. Round your answer to the nearest tenth.
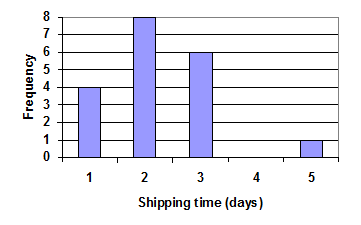
Answer (click to Show/Hide)
1. Mean: $\frac{1 \cdot 4 + 2 \cdot 8 + 3 \cdot 6 + 5 \cdot 1}{19} \approx 2.26$ or approximately 2.3.
2. Median: There are 19 values, so the position of the median in the ordered list of the data is found by calculating $\frac{19}{2} = 9.5$ and rounding up to the nearest integer. The median is located in the tenth position. From the chart we see the tenth position would fall in the bar with 2 as the label. The medain would be 2.
3. The mode would be 2 as that bar has the highest frequency which means we observe the data value 2 the most times.
Make up three data sets with 5 numbers each that have:
1. the same mean but different medians.
2. the same median but different means.
3. What observations can you make about the mean and median from this exercise?
Do you think it is important to see the distribution of that data along with the measure of center? Why or why not?
Create a scenario for which presenting the mean may be bias in understanding a set of data (include your data and the mean calculation and why that measure of center may not give a fair representation of the center for the data).
Is the student correct or not – explain your answer. John saw that there were five students who scored a 10 on the quiz and three that scored a 8. He adds up 8 and 10 to get 18 and divides by two and stated that the mean is 9.

Answer (click to Show/Hide)

John is incorrect in his approach. Each time we observe a 10 or 8 we need to factor that into the mean formula to find where the data balances. If you were to put the numbers 10 and 8 on a number line they would balance at 9, but if we add 5 10’s and 3 8’s the 10 side would be heavier and we would no longer balance at the value of 9.

The mean would be: $\frac{10 + 10 + 10 + 10 + 10 + 8 + 8 + 8}{8} = 9.25$
Your younger brother comes home one day after taking a science test. He says that someone at school told him that “60% of the students in the class scored above the median test grade.” What is wrong with this statement? What if he said “60% of the students scored below the mean?”
There are five values for a data set written on a sheet of paper along with the mean of 10 that was calculated. The values that we can read are 8, 12, 10, and 7. What is the missing data value?

Answer (click to Show/Hide)

There are a few approaches we can use. One is thinking of the balancing board over 10. Right now the 10 when on the board would just sit over the mean and the 8 and 12 are both 2 units from the mean, so they balance each other out. The last data point of 7 would need something of equal distance from the mean on the opposite side (3 units above the mean of 10), so 13 is the missing data value.

Our other approach will use algebra and the mean formula where we put in x to reprsent the missing data value:

$\begin{array}{l} \frac{8 + 12 + 10 + 7 + x}{5} = 10 \\ \frac{37 + x}{5} = 10 \\ 37 + x = 10 \cdot 5 \\ 37 + x = 50 \\ x = 50 - 37 \\ x = 13 \end{array}$

Attributions

This page contains modified content from David Lippman, “Math In Society, 2nd Edition.” Licensed under CC BY-SA 4.0.

This page contains modified content from “Collecting Data” by Foster et al., LibreTexts is licensed under CC BY-NC-SA 4.0.

This page contains modified content from “OpenStax Introductory Statistics” by Barbara Illowsky, Susan Dean. Licensed under CC BY 4.0.

This page contains content by Robert Foth, Math Faculty, Pima Community College, 2021. Licensed under CC BY 4.0.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

37	33	33	32	29	28	28	23	22	22	22	21	21	21	20	20
19	19	18	18	18	18	16	15	14	14	14	12	12	9	6

37	33	33	32	29	28	28	23	22	22	22	21	21	21	20	20
19	19	18	18	18	18	16	15	14	14	14	12	12	9	6

37	33	33	32	29	28	28	23	22	22	22	21	21	21	20	20
19	19	18	18	18	18	16	15	14	14	14	12	12	9	6

37	33	33	32	29	28	28	23	22	22	22	21	21	21	20	20
19	19	18	18	18	18	16	15	14	14	14	12	12	9	6

Calculating the Mean

Solution

Solution

Solution

Solution

Calculating the Median

Solution

Solution

Solution

Solution

Solution

Median vs Mean

Mode

Solution

Exercises

Attributions

License

Share This Book

37	33	33	32	29	28	28	23	22	22	22	21	21	21	20	20
19	19	18	18	18	18	16	15	14	14	14	12	12	9	6

37	33	33	32	29	28	28	23	22	22	22	21	21	21	20	20
19	19	18	18	18	18	16	15	14	14	14	12	12	9	6