3.2 The Square of Opposition

We have now established the boundaries of our domain of logically well-behaved natural language — A, E, I, and O propositions. These four types of categorical propositions are related to one another in systematic ways; we will look into those relationships.

---

3.2.1 Introducing the Square

The relationships are inferential: for example, we can often infer from the truth of one of the four types, whether the other three are true or false. These inferential relationships among the four categorical propositions are summarized graphically in a diagram known as The Square of Opposition. The diagram looks like this:

 

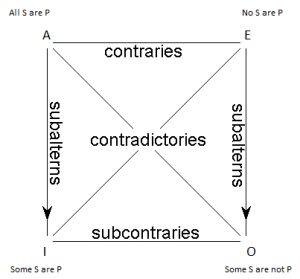
The four types of categorical propositions are arranged at the four corners of the square, and the relationships that apply between pairs of the proposition types are marked along the sides and diagonals.

First we will look at each of these four relationships:

• Contradictories
• Contraries
• Subcontradictories
• Subalterns

After that, we will work with inferences that can be made, if we know the truth status of one proposition type (e.g., an A proposition), about the truth/falsehood of the other three proposition types.

---

3.2.2 Contradictories

Contradictory pairs of categorical propositions are at opposite corners from one another on the Square of Opposition. A and O propositions are contradictory; E and I propositions are contradictory. What it means for a pair of propositions to be contradictory is this: they have opposite truth-values; when one is true, the other must be false, and vice versa.

This is pretty intuitive. Consider an A proposition—all sailors are pirates. Suppose I make that claim. How do you contradict me, how do you prove I’m wrong? My brother’s in the Navy, you might protest. He’s a sailor, but he’s not a pirate. That would do the trick. The way you contradict a universal affirmative claim—a claim that all S are P—is by showing that there’s at least one S (a sailor in this case, your brother) who’s not a P (not a pirate, as your brother is not). At least one S that’s not a P—that’s just the particular negative, O proposition, that some S are not P. (Remember: ‘some’ means ‘there is at least one’.) A and O propositions make opposite, contradictory claims. If it’s false that all sailors are pirates, then it must be true that some of them aren’t; that’s just how you show it’s false. Likewise, if it’s true that all dogs are animals (it is), then it must be false that some of them are not (you’re not going to find even one dog that’s not an animal). A and O propositions have opposite truth-values.

Likewise for E and I propositions. If we claim that no saints are priests, and someone wants to contradict, what they need to do is come up with a saint who was a priest. It’s not hard: Saint Thomas Aquinas (who was the most prominent medieval interpreter of Aristotle, by the way, and a terrific philosopher in his own right) was a priest. So, to contradict a universal negative claim—that no S are P—you need to show that there’s at least one S (a saint in this case, Thomas Aquinas) who is in fact a P (a priest, as Aquinas was). At least one S that is a P—that’s just the particular affirmative, I proposition, that some S are P. (Again, ‘some’ means ‘there is at least one’.) E and I propositions make opposite, contradictory claims. If it’s false that no saints are priests, it must be true that some of them are; that’s just how you show it’s false. Likewise, it’s true that no cats are dogs (it is), then it must be false that some of them are (you’re not going to find even one cat that’s a dog). E and I propositions have opposite truth-values.

---

---

3.2.3 Contraries

The two universal propositions—A and E, along the top of the Square—are a contrary pair. This is a slightly weaker form of opposition than being contradictory. Being contrary means that they can’t both be true, but they could both be false—though they needn’t both be false; one could be true and the other false.

Again, this is intuitive. Suppose I claim the universal affirmative, All dogs go to heaven, and you claim the corresponding universal negative, No dogs go to heaven. (Those sentences aren’t in standard form, but the translation is easy.) Obviously, we can’t both be right; that is, both claims can’t be true. On the other hand, we could both be wrong. Suppose getting into heaven, for dogs, is the way they say it is for people: if you’re good and all that, then you get in; but if you’re bad, oh boy—it’s the Other Place for you. In that case, both of our claims are false: some dogs (the good ones) go to heaven, but some dogs (the bad ones, the ones who bite kids, maybe) don’t. But that picture might be wrong, too. I could be right and you could be wrong: God loves all dogs equally and they get a free pass into heaven. Or, I could be wrong and you could be right: God hates dogs and doesn’t let any of them in; or maybe there is no heaven at all, and so nobody goes there, dogs included.

---

---

3.2.4 Subcontraries

Along the bottom of the Square, we have the two particular propositions—I and O—and they are said to be subcontraries. This means they can’t both be false, but they could both be true—though they needn’t be; one could be true and the other false.;

It’s easy to see how both I and O could be true. As a matter of fact, some sailors are pirates. That’s true. Also, as a matter of fact, some of them are not. It’s also easy to see how one of the particular propositions could be true and the other false, provided we keep in mind that ‘some’ just means ‘there is at least one’. It’s true that some dogs are mammals—that is, there is at least one dog that’s a mammal—so that I proposition is true. In fact, all of them are—the A proposition is true as well. This means that since A and O are contradictories, the corresponding O proposition—that some dogs are not mammals—must be false. Likewise, it’s true that some women are not (Catholic) priests (at least one woman isn’t a priest); and it’s false that some women are priests (the Church doesn’t allow it). So O can be true while I is false.

It’s a bit harder to see why both particular propositions can’t be false. Why can’t ‘Some surfers are priests’ and ‘Some surfers are not priests’ both be false? It’s not immediately obvious. But think it through: if the I (some surfers are priests) is false, that means the E (no surfers are priests) must be true since I and E are contradictory; and if the O (some surfers are not priests) is false, that means the A (all surfers are priests) must be true since O and A are contradictory. That is to say, if I and O were both false, then the corresponding A and E propositions would both have to be true. But, as we’ve seen already, this is (obviously) impossible: if I claim that all surfers are priests and you claim that none of them are, we can’t both be right.

---

---

3.2.5 Subalterns

The particular propositions at the bottom of the table—I and O—are subalterns of the universal propositions directly above them—A and E, respectively. (The universal propositions are called superalterns.) This means that the pairs have the following relationship: if the universal proposition is true, then the particular proposition (it’s subaltern) must also be true. That is, if an A propositions is true, it’s corresponding I proposition must also be true; if an E proposition is true, its corresponding O proposition must also be true.

This is intuitive if we keep in mind, as always, that ‘some’ means ‘there is at least one’. Suppose the A proposition that all whales are mammals is true (it is); then the corresponding I proposition, that some whales are mammals, must also be true. Again, ‘some whales are mammals’ just means ‘at least one whale is a mammal’; if all of them are, then at least one of them is! Similarly, on the negative side of the square, if it’s true that no priests are women (universal negative, E), then it’s got to be true that some priests are not women (particular negative, O)—that at least one priest is not a woman. If none of them are, then at least one isn’t!

Notice that these relationships are depicted in a slightly different way from the others on the Square of Opposition — there’s an arrow pointing toward the bottom. This is because the relationship is not symmetrical. If the proposition on top is true, then the one on the bottom must also be true; but the reverse is not the case. If an I proposition is true—some sailors are pirates—it doesn’t follow that the corresponding A proposition—that all sailors are pirates—is true. Likewise, the truth of an O proposition—some surfers are not priests—does not guarantee the truth of the corresponding E proposition—that no surfers are priests. (This could be true, but there is no guarantee. that there isn’t a surfing priest out there.)

Truth, as it were, travels down the side of the Square. Falsehood does not: if the universal proposition is false, that doesn’t tell us anything about the truth or falsehood of the corresponding particular. You could have a false A proposition—all men are priests—with a true corresponding I—some men are priests. But you could also have a false A proposition—all cats are dogs—whose corresponding I—some cats are dogs—is also false. Likewise, you could have a false E proposition—no men are priests—with a true corresponding O—some men are not priests. But you could also have a false E proposition—no whales are mammals—whose corresponding O— some whales are not mammals—is also false.

Falsehood doesn’t travel down the side of the Square, but it does travel up. That is, if a particular proposition—I or O—is false, then its corresponding universal proposition—A or E, respectively—must also be false. Think about it in the abstract: if it’s false that some S are P, that means that there’s not even one S that’s also a P; well, in that case, there’s no way all the Ss are Ps! False I, false A. Likewise on the negative side: if it’s false that some S are not P, that means you won’t find even one S that’s not a P, which is to say all the Ss are Ps; in that case, it’s false that no S is P (A and E are contraries). False O, false E.

---

---